Fetyloi's 《神经网络与深度学习》 学习笔记

附上我的语雀文档链接吧，导出的.md文件貌似不太好使：
https://www.yuque.com/yuqueyonghucoit3e/wefx9h/dlk9gxsk9fbg91uq?singleDoc# 《《神经网络与深度学习》（邱锡鹏）》 密码：bz42
第1章 绪论

1.表示学习

①表示学习：自动将输入信息转换为有效的特征，提高最终模型性能。

②语义鸿沟：输入数据的底层特征和高层语义信息之间的不一致性和差异性。

③嵌入：用神经网络将高维局部表示空间映射到非常低维的分布式表示空间，并尽可能保持不同对象间的拓扑关系。

2.深度学习

①深度学习：原始数据特征进行多步特征转换，得到特征表示，进一步输入到预测函数，得到最终结果。

②深度：原始数据进行非线性特征转换的次数。

3.赫布型学习

赫布型学习：俩神经元总相关联地受到刺激，使得它们之间的突触强度增加。

第2章 机器学习概述

1.机器学习三要素

模型、学习准则、优化算法

2.线性模型与非线性模型

线性模型的假设空间为一个参数化的线性函数族；

广义的非线性模型可以写为多个非线性基函数的线性组合。

3.损失函数

> 0-1损失；平方损失（不适用分类）；交叉熵损失（一般用于分类）；Hinge损失函数 >

4.优化问题与优化算法

优化问题与优化算法

优化问题：参数优化、超参数优化

优化算法：梯度下降、提前停止、随机梯度下降、小批量梯度下降

（.提前停止：在快要发生过拟合的时候停止迭代——使用验证集，在验证集上错误率不再下降就停止迭代）

超参数

超参数：定义模型结构或优化策略的一类参数

常见超参数：聚类中类别个数、梯度下降中学习率/步长，正则化项系数，神经网络层数，SVM核函数

5.参数估计方法

> 经验风险最小化、结构风险最小化、最大似然估计、最大后验估计 >

经验风险最小化–>过拟合–>结构风险最小化–>正则化

6.偏差-方差分解

偏差-方差分解的目的是：在模型拟合能力和复杂度之间取得较好平衡

降低偏差：增加数据特征、提高模型复杂度、减小正则化系数

降低方差：降低模型复杂度、加大正则化系数、引入先验、集成模型

7.数据的特征表示

> 图像特征、文本特征 >

图像特征表示：每一维的值为图像中对应像素的灰度值

文本特征表示——词袋模型：

①思想：向量表示，向量维度为与词表大小相同，向量第i维值为1表示词表第i个词在向量中出现

②缺点：不考虑词序，不能精确表示文本信息

③改进：使用N元特征——每N个连续词构成一个基本单元再放进词袋模型

8.传统特征学习【亦称维数约简/降维】

> **特征选择、特征抽取** >

特征选择：保留有用的、去除没用的，方法有子集搜索、正则化等：

①子集搜索：

i.过滤式方法：每次增加最有信息量（信息增益高）/删除最没信息量（信息增益低）的特征

ii.包裹式方法：每次增加对模型预测效果提升最有用/删除对模型预测效果提升最没用的特征

【从空增加是前向搜索，从原始特征集合删是反向搜索】

②正则化：会导致稀疏特征，因此间接实现了特征选择

特征抽取：原始特征投影到新的特征空间得到新表示，方法有监督和无监督：

①监督方法：eg.线性判别分析LDA

②无监督方法：eg.主成分分析PCA；自编码器AE

9.指标

准确率、错误率、精确率（查准率）、召回率（查全率）、F值、宏平均、微平均、交叉验证。。。

10.理论和定理

> PAC学习理论（可能近似正确学习理论）、没有免费的午餐定理、奥卡姆剃刀原理、丑小鸭定理、归纳偏置（贝叶斯中的先验） >

①可能近似正确学习理论：就是模型泛化错误小到一个差不多的程度ε就行，而且能以一定概率1-δ（也就是有可能）学到这个模型。从而得出了一个公式描述，如果固定了上面所说的ε和δ，可以得出学习需要的样本数量。

②没有免费的午餐定理：任何算法都有局限性，如果算法对某个问题有效，那么对一些其他问题一定比纯随机算法要差

③奥卡姆剃刀原理：如果俩模型性能相近，选简单的那个

第3章 线性模型

1.Logistic回归（逻辑斯谛回归/对数几率回归）

Logistic回归采用交叉熵作为损失函数，可用梯度下降法、牛顿法等来优化参数

2.Softmax回归（多项/多类的Logistic回归）

Softmax回归也采用交叉熵作为损失函数。Softmax回归核心是应用Softmax函数将线性模型的输出转化为一个类别概率分布，其中Softmax函数会将每个类别计算得到的分数转换为概率

3.感知器

二分类：普通感知器-->投票感知器-->平均感知器

多分类：广义感知器

逻辑：

感知器学习的参数和训练样本顺序相关：根据前面的样本学好了，预测很不错，结果在最后一个错了，更新参数，反而学的参数变差了。

解决这种问题需要提高感知器鲁棒性和泛化能力，给每个参数一个置信系数，最终分类结果由不同参数的感知器投票决定——投票感知器。

投票感知器对参数的保存记录有开销，因此通过参数平均策略减少参数数量——平均感知器

4.支持向量机

【大部分都已经学习过了 不重复写入】

第4章 前馈神经网络

1.激活函数：

①Sigmoid型函数：(Hard)Logistic/(Hard)Tanh

②ReLU函数：带泄露的/带参数的/ELU/Softplus

③Swish函数

④GELU函数

⑤Maxout单元

2.网络结构：前馈/记忆/图

3.反向传播：

①前馈计算每层净输入和激活值，直到最后一层

②反向传播计算每一层的误差项

③计算每一层参数的偏导数

4.自动梯度计算：数值微分/符号微分/自动微分

5.详细与补充

①误差项：目标损失函数关于某层的神经元（的净输入）的偏导数，用δ(l)来表示。

②数值微分就是取很少的非零扰动Δx计算梯度，符号微分就是通过迭代或递归使用一些事先定义好的规则进行变换。

③自动微分可分为前向模式和反向模式，前向按照计算图中的计算方向递归计算梯度，反向按照相反方向、与反向传播计算梯度的方式相同。都是基于链式法则的。

第5章 卷积神经网络

1.卷积咋算，一维卷积和二维卷积是啥，卷积核/滤波器是啥

①卷积核/滤波器就是信息的衰减率，每个时刻的信号乘上各自对应的衰减率，再加一起，就是卷积。标准来讲，信号序列和滤波器/卷积核的卷积定义为y=w*x，*就是卷积运算。

②一维卷积就是信号序列是一行，二维卷积就是信号序列是一个二维表，二维卷积的算法就是从这个表里找到和卷积核表一样大小的一块区域，并对应卷积核表的相对位置，每个数都按位去乘起来，然后加起来得到这个数放到刚才说的对应位置里，其中在乘之前，需要把卷积核翻转一下。

③特征映射的概念：一幅图像卷积后得到的结果。

2.卷积和互相关是啥关系

互相关和卷积的区别是卷积核是否翻转，互相关也可以称为不翻转卷积。

3.卷积的步长、零填充是干啥的

步长是卷积核滑动时的时间间隔，零填充是在输入向量两端进行补0，根据不同步长和填充有常用卷积：窄/宽/等宽卷积

4.卷积的数学性质

卷积的数学性质是交换性和导数。

其中导数说的是：卷积后通过激活函数，这个激活值关于输入序列的偏导，等于其对卷积的偏导和卷积核的卷积结果

5.卷积神经网络的构成，三个部分分别干啥的

卷积层：提取局部区域特征，不同卷积核是不同的特征提取器；

汇聚层：选择特征、降低特征数量，从而减少参数数量。

汇聚层汇聚函数常用的有最大汇聚和平均汇聚，分别是取区域内神经元最大活性值和平均活性值。就是说，卷积层提取特征，汇聚层把特征压缩从而减少参数量。

【汇聚层=池化层; 最大/平均汇聚=最大/平均池化】

全连接层

6.卷积网络的参数学习，也就是卷积网络的反向传播咋进行的，学习的参数是哪些

学习的参数是卷积核和偏置，汇聚层和卷积层反向传播的不同在于误差项的计算不同

7.典型的卷积神经网络

> LeNet-5,AlexNet,Inception 网络,残差网络 >

①LeNet-5网络：值得注意的是用了连接表来定义输入和输出特征映射之间的依赖关系

【连接表：写出来关系，从而指导我们，让每一个输出特征都依赖于少数几个特征映射】

②AlexNet网络：将网络拆成两半分别放在俩GPU上

③Inception网络：特点是一个卷积层包含多个不同大小的卷积操作

④残差网络：思想是在用非线性单元逼近目标函数时拆分一下，h(x)=x+(h(x)-x)，前后两项分别是恒等函数和残差函数，让非线性单元近似残差函数简单点，然后+x就逼近了目标函数

9.其他卷积方式：转置卷积、微步卷积、空洞卷积都分别是干啥的

①转置卷积：转置的是卷积核，作用是实现低维到高维的反向映射

②微步卷积：想让步长小于1从而提高特征维数，但是步长没法小于1，所以在输入特征之间插入0间接减小步长

③空洞卷积：给卷积核加入一些空洞来增加卷积核的大小，从而能够不增加参数数量，同时增加输出单元感受野

【感受野：神经元只接受其所支配的刺激区域内的信号，只有这个区域内的刺激才能激活该神经元】

第6章 循环神经网络

1.延时神经网络TDNN、有外部输入的非线性自回归模型NARX、循环神经网络RNN，三者分别是啥概念，之间有啥不同点和联系

三者的概念

**TDNN**给前馈网络非输出层加了延时器，延时器可以记录神经元最近几次活性值，l层活性值依赖于l-1层神经元最近K个时刻的活性值；

NARX也用延时器，延时器记录最近几次的外部输入和最近几次的输出，把这些输入、输出传入一个非线性函数，得到某时刻的输出；

RNN用了带自反馈的神经元，将前一个活性值（由延迟器记录）和当前输入序列传入非线性函数，从而更新带反馈边的隐藏层的活性值（称为状态/隐状态）

三者的联系

**TDNN**仅依赖固定窗口的输入，不能捕捉长时间依赖，不使用反馈。

NARX显式依赖过去的输入和输出，有反馈机制，能处理短期依赖的输入-输出关系。

RNN通过隐藏状态隐式记忆所有历史信息，能处理长时间依赖，但训练复杂。

TDNN适合处理短期依赖和固定窗口长度的任务，NARX适用于有明确输入输出关系，RNN适合处理复杂、长依赖关系的任务

2.从简单循环网络SRN理解RNN的具体原理

SRN=两层前馈神经网络+隐藏层到隐藏层的反馈连接。隐藏层状态的计算见笔记图。

3.图灵完备是什么概念

图灵完备：可以实现图灵机的所有功能的数据操作规则称为图灵完备，如主流编程语言。

p.s. 所有的图灵机都可以被一个由sigmoid型激活函数的神经元构成的全连接RNN来进行模拟

4.RNN应用到不同类型机器学习任务对应的三种模式：序列到类别模式、同步的序列到序列模式、异步的序列到序列模式

①序列到类别模式：输入为序列，输出为类别。将整个序列的最终表示传入分类器进行分类。最终表示可以选最后时刻的状态，也可以选择整个序列所有的状态的平均（一个平均状态）

②同步的序列到序列模式：每一时刻都有输入和输出，输入序列和输出序列长度相同。例如用于词性标注。

:::info
一个疑问：词性标注似乎只取决于当前词本身，而与上下文无关，为什么要采取RNN呢？

对应的解释：

a.多义词： 很多词具有多个词性，其确切词性往往取决于上下文。例如“银行”可以是名词（去银行办业务），也可以是动词（银行贷款）。

b.同形异义词： 不同的词可能具有相同的形式，但词性不同。例如“打”可以是动词（打篮球），也可以是量词（一打啤酒）。

c.长距离依赖： 词性标注有时需要考虑较长的上下文信息。例如，一个代词的词性往往取决于它所指代的名词，而这个名词可能出现在较远的前面。

:::

③异步的序列到序列模式（编码器-解码器模型）：输入序列输出序列不一定严格对应，也不一定长度相等。编码器和解码器是两个不同的RNN，样本x按不同时刻输入编码器得到编码，再把编码传入解码器得到输出序列

5.RNN怎么进行参数学习—梯度下降—BPTT/RTRL

RNN的参数学习BPTT和RTRL见图。BPTT计算少，但要存所有时刻中间梯度，空间复杂度高；RTRL不需要梯度回传。

6.什么是梯度爆炸问题，什么是梯度消失问题，什么是长程依赖问题，怎么解决这些问题

①长程依赖问题：时刻t的输出依赖时刻k的输入，但t和k间隔很长，神经网络很难建模这种长距离依赖关系，称长程依赖问题。为什么难建模，是因为t和k间隔很长的情况下，引发梯度爆炸问题和梯度消失问题。【梯度爆炸问题、梯度消失问题见上图】

②怎么解决：

梯度爆炸——权重衰减（正则化，限制参数取值范围使γ<=1）/梯度截断（大于阈值就截断成较小的数）；

梯度消失——改变模型；为了解决俩问题，引入门控机制。

7.基于门控的RNN：什么是长短期记忆网络LSTM，什么是长短期记忆，LSTM的变体

①引入内部状态、候选状态、门控机制

a. LSTM引入的内部状态：专门进行线性的循环信息传递，同时（非线性地）输出信息给隐藏层的外部状态；

b. LSTM引入的候选状态：从非线性函数输出得到。

  c. 门控机制：输入门（控制当前时刻候选状态要保存多少信息）、遗忘门（控制上一时刻内部状态要遗忘多少信息）、输出门（控制当前时刻内部状态有多少要输出给外部状态）。三个门取值都在0，1之间表示以一定比例让信息通过。

②长期记忆：隐含从训练数据学到的经验，更新周期远远慢于短期记忆。长短期记忆的生命周期介于长期记忆和短期记忆之间。

③LSTM变体：

a.无遗忘门的；

b.三个门不但依赖于输入和上一时刻的隐状态，也依赖于上一个时刻的记忆单元的peephole连接；

c.耦合输入门和遗忘门（因为在LSTM中这两个门有一定的互补关系，所以合并成一个）

8.基于门控的RNN：门控循环单元网络GRU

GRU：不引入额外记忆单元，引入更新门——控制当前状态需要从历史状态中保留多少信息（不经过非线性变换，以及需要从候选状态中接受多少新信息。

更新门=0时当前状态和前一时刻状态间为非线性函数关系；=1时为线性函数关系。引入重置门控制候选状态的计算是否依赖上一时刻状态。

重置门=0时候选状态只与当前输入有关，与历史无关；重置门=1时与当前输入和历史都有关，和简单RNN一致

9.什么是深层RNN，怎么增加RNN的深度（堆叠RNN，双向RNN）

单看网络输入到输出间路径，RNN很浅。

增加深度以增强RNN能力，方式主要是增加同一时刻网络输入到输出间路径。

①堆叠RNN：第l层网络输入是第l-1层网络输出，每层内部计算自己时时刻刻的隐状态。

②双向RNN：增加按时间逆序传递信息的网络层。有两层RNN构成，两个的输入相同，信息传递方向不同。

10.RNN扩展到图结构：递归神经网络RecNN与图神经网络GNN

①RecNN：RNN在有向无循环图上的扩展

②GNN：将消息传递的思想扩展到图数据结构上，每个节点可以接收相邻节点消息并更新自己状态

【消息传递思想：隐状态看作节点，节点收到父节点的消息，更新自己状态，传递给子节点】

第7章 网络优化与网络正则化

一、网络优化问题

> 网络优化问题——找到更好的局部最小值（平坦的）和提高优化效率 >

1.从算法的优化出发，用更有效的优化算法：着眼于批量大小 / 学习率 / 梯度估计

（1）批量大小的选择：

批量小：越有可能收敛到平坦最小值，，但需要设置较小学习率，否则模型会不收敛

批量大：训练稳定，可设置较大学习率，但越有可能收敛到尖锐最小值

批量大小较小时，可采用线性缩放准则【批量大小增加m倍时学习率也增加m倍】

=>适当小批量

（2）学习率的调整：

①学习率衰减（学习率退火）

概念：经验上，学习率开始时保持大些以保证收敛速度，收敛到最优附近时小些以避免振荡

方法：分段常数衰减（阶梯衰减）/ 逆时衰减 / 指数衰减 / 自然指数衰减 / 余弦衰减

②学习率预热：

Why：批量大时，需要较大学习率，但开始时梯度也大，初始学习率也大的话，训练不稳定

概念：开始时用小学习率，梯度下降到一定程度后再恢复初始学习率

方法：逐渐预热【按迭代次数从比较小的学习率逐渐增大，直至回到初始学习率】

③周期性学习率调整：

Why：参数在尖锐最小值，增大学习率有助于逃离；在平坦最小值，增大后依然可能在其吸引域内

概念：周期性增大学习率

方法：循环学习率【让学习率在一个区间内周期性增大/缩小】【if线性缩放=>三角循环学习率】

带热重启的随机梯度下降【每间隔一定周期，学习率重新初始化为某预先设定值，然后衰减】

④AdaGrad算法：

概念：每次迭代时先计算每个参数梯度平方累计值，效果上累计大的学习率小，累计小的学习率大

【但整体学习率随迭代次数增加而缩小】

缺点：if迭代多次还没找到最优点，那基本没希望了，因为学习率已经被搞得很低了

⑤RMSprop算法：

与AdaGrad区别：不算累计，算每次迭代的梯度平方的指数衰减移动平均

优点：每次迭代，每个参数学习率并不一定衰减，可能小可能大。

⑥AdaDelta算法：

与AdaGrad和RMSprop区别：不仅用梯度平方的指数衰减移动平均来调整学习率，还引入每次参数更新差值的平方的指数衰减权移动平均

优点：在一定程度上平抑了学习率的波动

【将RMSprop中的初始学习率改为动态计算的参数更新插值的平方的指数衰减权移动平均】

（3）梯度估计修正【cuz每次迭代的梯度估计和整个训练集上的最优梯度并不一致，具有随机性】

①动量法：

概念：计算负梯度的“加权移动平均”作为参数的更新方向；相当于模拟物理中动量的概念

效果：参数实际更新差值取决于最近一段时间内梯度的加权平均值

【方向一致，参数更新幅度大，加速；方向不一致，梯度更新幅度小，减速】

②Nesterov加速梯度（Nesterov动量法）

概念：对动量法的改进。改进在“负梯度”是对谁的梯度。

改进：动量法分两步：

根据上一步参数更新方向更新一次得到参数theta hat；

再用当前梯度的反方向进行更新。

问题在于当前梯度说的还是上一时刻的梯度，而不是theta hat的梯度，改为后者更合理。

③Adam算法：

概念：可看作动量法和RMSprop的结合，使用动量作为参数更新方向，且自适应调整学习率

计算：梯度平方的指数加权平均【类似RMSprop】+梯度的指数加权平均【类似动量法】

  分别看作：梯度均值 和 未减去均值的方差。迭代初期值比真实小，偏差大，因此需做修正

进一步的改进：引入Nesterov加速梯度，称为Nadam算法

④梯度截断：

概念：梯度爆炸时，梯度的模大于一定阈值，对梯度进行截断

方法：按值截断【超过区间，梯度就设为区间上限；低于区间，梯度就设为区间下限】

按模截断【截断到一个给定的截断阈值b】

2.从参数初始化的角度出发，用更好的参数初始化方法：

（1）预训练初始化：

①概念：用已经在大规模数据上训练过的模型提供的参数初始值

②优点：通常具有更好的收敛性和泛化性

③缺点：灵活性不够，不能任意调整网络结构

（2）固定值初始化：

概念：对特殊参数，根据经验，用特殊固定值，初始化

（3）随机初始化：

①概念：避免全初始化为0导致的对称权重现象，对每个参数随机初始化，提高不同神经元间区分性

②基于固定方差的参数初始化：

概念：从固定均值&方差的分布中采样，生成参数初始值

方法：高斯分布初始化【用高斯分布𝒩(0, 𝜎2)】

均匀分布初始化【[−𝑟, 𝑟] 内采用均匀分布】

问题：参数范围太小【导致神经元输出过小、Sigmoid型激活函数丢失非线性能力】

      	参数范围太大【导致输入状态过大、Sigmoid激活值饱和，梯度消失】

解决：配合逐层归一化

③基于方差缩放的参数初始化：

概念：根据神经元的连接数量自适应调整初始化分布的方差

【输入连接多，每个输入连接上的权重就应该小些，避免输出过大或过饱和/// vise versa】

方法：Xavier初始化【根据 𝑀𝑙−1 + 𝑀𝑙（分别是𝑙−1和𝑙 层神经元数量）初始化参数𝑙 层方差】

【适用激活函数：恒等函数、Logistic函数、Tanh函数】

      He初始化【使用ReLU函数时通常一半神经元输出为0，分布的方差近似为恒等函数一半】

④正交初始化：

概念：将某层的权重矩阵初始化为正交矩阵

原因：用正交矩阵的性质，保证传播过程的范数保持性

步骤：用均值为0方差1的高斯分布初始化一个矩阵

by奇异值分解得两个正交矩阵，用其一作为权重矩阵

3.数据预处理

（1）尺度不变性：算法缩放全部/部分特征后不影响学习和预测

尺度敏感：影响

=>对样本预处理，各维特征转换到相同取值区间，消除不同特征相关性

（2）归一化：把数据特征转换为相同尺度

方法：最小最大值归一化 / 标准化（Z值归一化）/ 白化

4.逐层归一化

（1）概念：数据归一化应用到神经网络中隐藏层的输入中

（2）Why：

①更好的尺度不变性：低层参数改变不影响高层输入保持稳定+更高效进行参数初始化和超参选择

②更平滑的优化地形：优化地形平滑，梯度稳定，允许更大学习率，提高收敛速度

（3）常用方法：批量归一化 / 层归一化 / 权重归一化 / 局部响应归一化

5.超参数优化

（1）超参数

①网络结构【神经元间连接关系、层数、每层神经元数量、激活函数类型】

②优化参数【优化方法、学习率、小批量样本数量】

③正则化系数

（2）简单方法

①网格搜索：尝试所有超参组合，分别训练模型，测试性能，选取最好的配置

②随即搜索：超参随机组合，然后思路同上

③贝叶斯优化：根据当前已实验的超参组合，预测下个可能最好的组合

Eg. 时序模型优化（SMBO）

需定义收益函数，Eg. 期望改善函数（EI函数）/ 改善概率 / 高斯过程置信上界（GP-UCB）

④动态资源分配：

思想：预先估计配置效果，差就中止评估，转而将资源留给其他配置

常用策略：早期停止策略

一种有效方法：逐次减半【但需要注意 超参数配置的数量N 的设置】

⑤神经架构搜索：通过神经网络来自动实现网络架构的设计

二、网络正则化问题

:::info """

在传统机器学习中常采用ℓ1 和 ℓ2 正则化来限制模型复杂度，避免过拟合；

但在训练深度神经网络，特别是过度参数化（模型参数数量远大于训练数据数量）时，用其他方法更好。

“”"

:::

1.ℓ1 和 ℓ2 正则化

> 就是在参数优化时加了一个λℓ(θ)，其中ℓ可以是一阶范数也可以是二阶范数，λ为正则化系数 >

（1）注意点1：ℓ1范数在零点不可导，需要用其他方式近似

（2）注意点2：ℓ1范数约束通常使优化出来的最优参数位于坐标轴上，使得最终参数为稀疏性向量（有好多0）

（3）注意点3：同时加入ℓ1和ℓ2正则化（相应的用两个正则化系数）称为弹性网络正则化

2.权重衰减

每次参数更新时引入衰减系数β，使得θt=(1-β)θt-1-αgt，gt是更新时梯度，α是学习率

3.提前停止

整一个验证集，验证集错误率不下降，就停止迭代优化，不继续下去了

4.丢弃法

随机丢弃神经元及其连接来避免过拟合，用掩蔽函数mask(·)来做这件事

（1）掩蔽函数做了啥：对于某层神经元的输入，训练阶段用丢弃掩码m来丢弃一些输入从而丢弃掉神经元及其连接（m由概率为p的伯努利分布随机生成）；测试阶段同样用概率p来乘所有输入来平衡被丢掉的和留下的输入

（2）集成学习角度的解释：每次迭代相当于训练一个不同的、共享原始网络参数的子网络；最终网络是子网络的集成

（3）贝叶斯学习角度的解释：（先验分布*网络）在所有参数上的积分，可以用M次dropout后的网络的算数平均来近似

（4）RNN上的dropout：

    ①对非时间维度的连接（非循环连接）进行随即丢失【时间维度记录了隐状态不能乱丢】

    ②变分丢弃法：对参数矩阵的每个元素进行随机丢弃，并且在所有时刻都要使用相同的丢弃掩码

5.数据增强

通过算法对数据转变来增加数据量，避免在小数据量数据集上过拟合了，方法有旋转/翻转/缩放/平移/加噪声等

6.标签平滑

在输出标签中添加噪声，比如一些错误标注了的样本，最小化这些样本上的损失函数就会导致过拟合，所以加噪

（1）注意点1：标签用one-hot表示可看作硬目标，softmax分类器+min交叉熵损失函数会导致正确类和其他类权重差异很大，导致过拟合，所以对标签的one-hot编码来加噪，变成软目标，避免模型输出过拟合到硬目标上

（2）注意点2：按照类别相关性来给不同标签不同的噪声概率，称为知识蒸馏

第8章 注意力机制与外部记忆

1.什么是注意力

（1）概念：有意或无意从大量输入中选择小部分有用信息来重点处理，并忽略其他信息的能力

（2）分类：聚焦式注意力/选择性注意力【自上而下的有意识的】、基于显著性的注意力【自下而上的无意识的】

2.注意力机制

> 作为一种资源分配方案，有限的计算资源用来处理更重要的信息 >

（1）计算方式

:::info 在所有输入信息上计算注意力分布，然后根据注意力分布来计算输入信息的加权平均

:::

  ①注意力分布：给定查询向量和输入向量集合，选择第n个输入向量的概率分布

  ②加权平均：计算（选择第n个输入向量的概率 * 第n个输入向量）的累加

（2）注意力机制变体

①硬性注意力：只关注某个输入向量，要么选取最高概率的输入向量，要么在注意力分布式上随机采样

:::info
无法用反向传播训练了，需要使用强化学习，所以一般用软性注意力【软性注意力就是（1）中的那种注意力】

:::

  ②键值对注意力：用键值对表示输入，键用来计算注意力分布，值用来计算聚合信息。这种方式的特殊点是输入信息的形式

  ③多头注意力：用多个查询向量，并行地从输入中选多组，这样使得每个注意力关注输入信息的不同部分

  ④结构化注意力：假设输入信息的重要程度存在差异，从而形成了层次结构

  ⑤指针网络：仅采用注意力机制的注意力分布作为软性指针，指出相关信息的位置，输出序列是输入序列的下标

3.自注意力（内部注意力）模型

> 为了建立输入序列之间的长距离依赖关系而使用 >

（1）思想

用注意力机制来“动态”生成不同连接的权重的全连接网络，注意动态生成的是不用连接的权重

（2）做法

采用QKV（查询-键-值）模式。先把每个输入映射到三个不同空间，分别得到了查询向量、键向量和值向量。然后用键值对注意力机制的原理（2.（2）.②），得到输出向量。

（3）用法

替换卷积层和循环层，也可以和这俩一起交替使用。

（4）缺点

忽略了输入信息的位置信息，单独使用时需要加入位置编码信息来进行修正

4.“记忆”的了解与认识

长期记忆与短期记忆与工作记忆

:::info
长期记忆类比人工神经网络中的权重参数，短期记忆类比人工神经网络中的隐状态

:::

记忆在大脑皮层是分布式存储而不是局部存储

联想记忆是基于内容寻址的存储

工作记忆是临时存放和某任务相关的短期记忆和其他相关的内在记忆；临时存储和处理系统；维持时间短；”缓存“；容量小

外部记忆是神经网络借鉴工作记忆原理引入的

5.记忆增强神经网络MANN

:::info **记忆增强神经网络MANN（记忆网络MN）：装备外部记忆的神经网络**

:::

（1）端到端记忆网络MemN2N

要存储的信息转换成两组记忆分别用于寻址和输出，然后主网络根据输入生成查询向量，用键值对注意力机制来读取记忆并产生输出。

【特点：外部记忆单元只读】

（2）神经图灵机NTM

控制器接收（当前输入+上时刻输出+上时刻读取外部记忆的信息），然后产生（当前输出+查询向量+删除向量+增加向量），然后开始读写。

读，从外部记忆读取信息，采用注意力机制来进行基于内容的寻址；

写，根据注意力分布按比例删除和增加每个记忆片段的删除向量和增加向量。

【特点：外部记忆可读写】

:::info
多跳操作：主网络根据上一次从外部记忆读取的信息，生成一个新的查询向量，而这个查询向量又继续用于读取外部记忆，这样循环多轮进行交互，从而可以实现更复杂的计算

:::

6.基于神经动力学的联想记忆

:::color2 是基于**内容**寻址的

应用：原理所对应的模型 or 用来增加外部记忆

两种联想记忆模型：

自联想模型：输入的模式与输出的模式在同一空间

	  		  eg.可通过前馈/循环神经网络等实现

异联想模型：输入的模式和输出的模式不在同一空间

	  	  eg.大多机器学习问题可看作异联想，可作分类器

:::

（1）Hopfield网络

:::info Hopfield网络是由一组互相连接的神经元组成的RNN。

【属于自联想模型；每个神经元既输入也输出，无隐藏神经元】

:::

①更新方式

异步更新【每次更新一个神经元，顺序可随机也可预先指定】

同步更新【一次性更新所有神经元，需要时钟】

②能量=每个不同的网络状态【是标量】；

网络收到外部输入后会演化到某个稳定状态

③稳定状态=吸引点Attractor=能量局部最优点=能量函数的局部最小点=网络中存储的模式Pattern

④检索：从接收到网络输入，随时间收敛到吸引点上的过程。

 【每个吸引点对应一个管辖区域，输入落到该区域会收敛到该点】

⑤存储容量怎么提升：改进网络结构、学习方式、引入更复杂的运算

（2）使用联想记忆增加网络容量

①将联想记忆模型作为部件引入LSTM网络

②将RNN的部分连接权重作为短期记忆，并通过一个联想记忆模型继续更新

第9章 无监督学习

1.无监督学习问题分类

（1）无监督特征学习

从无标签训练数据中挖掘有效特征/表示

用来降维、数据可视化、监督学习前期的数据预处理

（2）概率密度估计

根据一组训练样本来估计样本空间的概率密度

根据假设/不假设数据服从某个已知概率密度函数形式的分布，可以分为参数密度估计、非参数密度估计

（3）聚类

将一组样本根据一定的准则划分到不同的组（即簇）

eg.谱聚类、K-Means

2.无监督特征学习

（1）主成分分析PCA——数据降维方法

①思想：使得在转换后的空间中数据的方差最大，从而最大化数据差异性，保留更多原始数据信息

②手段：选择数据方差最大方向进行投影

③用处：作为监督学习的数据预处理方法，去除噪声并减少特征间相关性等

④局限性：不能保证投影后数据类别可分性更好

PCA更详细内容见下：

李航《机器学习方法》中关于PCA的部分：

第十六章 主成分分析

周志华《机器学习》中关于PCA的部分：

主成分分析

（2）稀疏编码

①编码是啥：对 𝐷 维空间中的样本 𝒙 找到其在 𝑃 维空间中的表示（或投影）

②怎么得到编码：得找到一组完备的基向量（例如主成分分析PCA找到的主成分/投影矩阵）

③啥是完备：M个基向量能支撑M维的欧氏空间，就是完备，能支撑比M还高维的，就是过完备

④为啥要稀疏：稀疏好啊，稀疏有优点：

a. 计算量上：极大地降低计算量

b. 可解释性上：将输入样本表示为少数几个相关特征，更好描述特征

c. 特征选择上：可以实现特征自动选择，自动是指只选择和输入样本最相 关的少数特征，能降低噪声，减轻过拟合

⑤怎么得到稀疏编码：得到编码，需要完备基向量，那稀疏编码，就需要过完备的基向量

⑥那怎么得到过完备基向量：

按照这个图来找到，其中：

𝒁 = [𝒛⁽¹⁾, ⋯ , 𝒛^(𝑁)]， 这个集合里面每个元素都是一组基向量的系数𝒛，

𝒛 = [𝑧1, ⋯ , 𝑧𝑀] ，𝒛 也称为一个输入样本 𝒙 的编码

【1个样本，对应1组基向量，一个系数集合𝒛】

𝜌(⋅) 是一个稀疏性衡量函数，𝒛 越稀疏，𝜌(𝒛) 越小，函数可以选择

                          ℓ1 范数 / 对数函数 / 指数函数

𝜂 是一个超参数，用来控制稀疏性的强度

（3）自编码器

①干啥的：（D维数据+自编码器）——映射—— 得到M维特征空间下，每个样本的编码

而这个编码，可以重构出原来的样本

自编码器可以得到有效的数据表示，例如最小重构错误、稀疏性等

②结构：编码器 f（把数据从D维映射到M维）

解码器 g（把数据从M维重构到D维）

③学习目标：既然是为了要重构原来的样本，就应该最小化重构错误

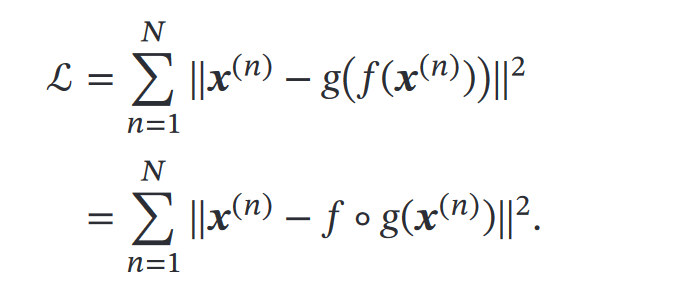
也就是最小化上面这个式子

④根据维度来讨论：

a. 𝑀 ≥ 𝐷：一定可以找到一组或多组解使得 𝑓 ∘ 𝑔 为单位函数并使得重构错误为 0

然后加一些约束，比如要求编码只能取K个不同值，那就转换为K类的聚类问题的解了

b. 𝑀 < 𝐷：相当于一种降维/特征抽取方法了

⑤简单自编码器：

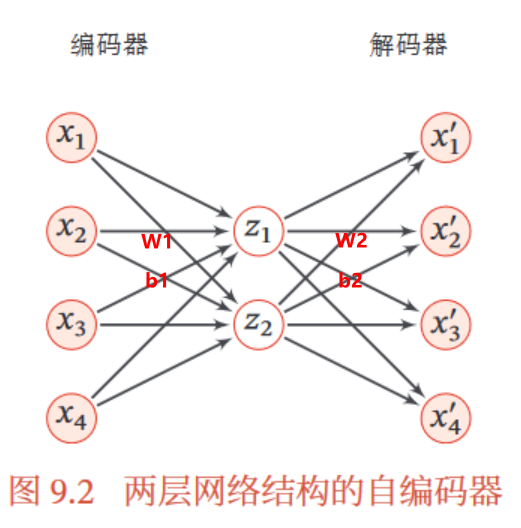
如果W2=W1的转置，就成为捆绑权重，这会使得自编码器参数少，更容易学习，还起到一定的正则化作用。

通过最小化重构错误 ℒ= ∑ ‖𝒙(𝑛) − 𝒙′(𝑛))‖2 + 𝜆‖𝑾 ‖2𝐹 . 学习网络参数

（4）稀疏自编码器

①概念：𝑀 > 𝐷，且让我们映射到的这个M维特征空间下，样本编码尽量稀疏

②学习目标：最小化重构错误，目标函数为ℒ= ∑ ‖𝒙(𝑛) − 𝒙′(𝑛))‖<sup>2</sup> + 𝜂𝜌(𝒁) + 𝜆‖𝑾 ‖<sup>2</sup>

其中稀疏性度量函数 𝜌(𝒁)可以有多种定义：

a. 利用“稀疏编码”一节中的公式，分别计算每个编码稀疏度，再求和

b. 定义为一组训练样本中，每一个神经元激活的概率

这个概率可用隐藏层某个神经元的**平均活性值**来近似

希望该平均活性值接近于事先给定的某值，用KL距离来衡量差异

KL(𝜌∗|| ̂ 𝜌𝑗) = 𝜌∗ log 𝜌∗ ̂ 𝜌𝑗 + (1 − 𝜌∗) log [(1 − 𝜌∗) / (1− ̂ 𝜌𝑗)]

所以也就是将稀疏性度量函数定义为 𝜌(𝒁) =  ∑ KL(𝜌∗|| ̂ 𝜌𝑗).

（5）堆叠自编码器

用逐层堆叠方式来训练一个深层的自编码器，采用逐层训练来学习网络参数

（6）降噪自编码器

①目的是干啥的：对数据部分损坏的鲁棒性——希望从坏了的数据中也能得到有效数据表示，恢复完整原始信息

②怎么达到的目的：引入噪声增加编码鲁棒性

③过程：向量x—按比例μ随机将部分维度值设为0—破损向量x—输入给自编码器—编码z—重构出无损原始输入x

3.概率密度估计

（1）参数密度估计

①概念：根据先验知识，假设随机变量服从某种分布，然后通过训练样本，估计分布的参数

②过程：第一，假设服从𝑝(𝒙;𝜃)这样一个概率分布函数

第二，求对数似然函数，也就是求个对数，log 𝑝(𝒟;𝜃) = ∑ log 𝑝(𝒙(𝑛);𝜃)

第三，最大似然估计MLE，寻找使log 𝑝(𝒟;𝜃)最大的𝜃，使参数估计问题变成了最优化问题

③会遇到的问题：

a. 这个概率密度函数的选取，可能不那么好选，因为实际数据分布往往复杂，不是简单的分布

b. 训练样本只包含部分可观测变量，有些关键变量无法观测到，就很难准确估计真实分布

c. 维数灾难，高维数据维数越高，参数估计问题所需要的样本就越多，样本不足时会过拟合

④常见的概率分布函数的选取：

a. 正态分布：要估计的参数是均值μ和方差Σ

b. 多项分布：要估计的参数是第k个状态的概率μ<sub>k</sub>和拉格朗日乘子λ

                   （引入拉格朗日乘子将问题转换成了无约束优化问题）

（2）非参数密度估计

①概念

不假设数据服从某种分布了，而是把样本空间划分成不同区域，估计每个区域的概率，近似数据的概率密度函数`𝑝(𝒙)`

每个区域的概率：𝑃<sub>𝐾</sub> = C<sup>𝑁</sup><sub>𝐾</sub> 𝑃<sub>𝐾</sub> (1 − 𝑃)<sup>1−𝐾</sup> 【二项分布】

N非常大时，近似：𝑃≈ 𝐾/𝑁

又假设区域足够小（V足够小），则内部概率密度均匀、相同：𝑃 ≈ 𝑝(𝒙)𝑉

然后我们就得到了𝑝(𝒙)≈ 𝐾/𝑁𝑉

②总结一下条件要求

**N足够大+V足够小**

但V过小：落入区域样本少，概率密度不准确

解决方案：

A. 固定区域大小V，统计落入不同区域的数量——直方图方法、核方法

B. 改变区域大小V，使得落入每个区域的样本数量都为K个——K近邻方法

③直方图方法


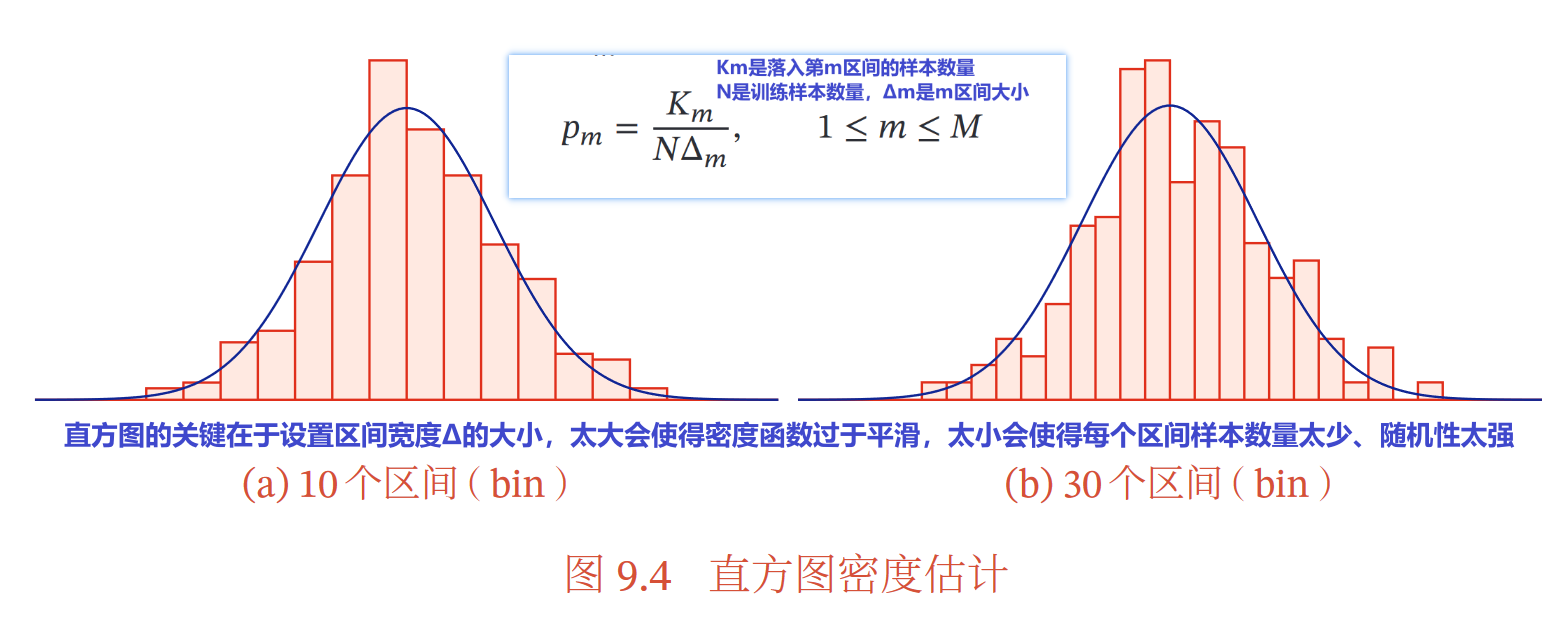优点：处理低维变量快速可视化数据分布

缺点：很难扩展到高维变量

需要的样本数量随维度增加而指数增长，导致维数灾难

④核方法（核密度估计，也叫 Parzen 窗方法）

原理就是定义核函数，如果落在核函数表示的空间内，核函数的值为1，否则为0，

从而每一个点的密度估计就可以用：

（落入区域的样本数量K、）训练样本数量N、核函数表示空间的边长H来得到

超立方体核函数


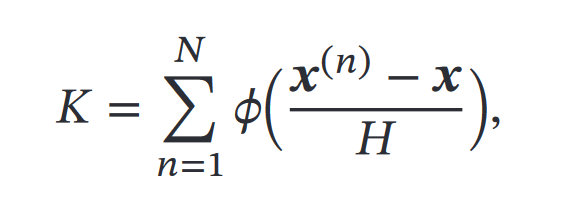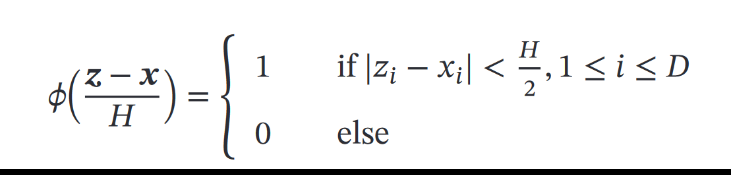然后就得到了：

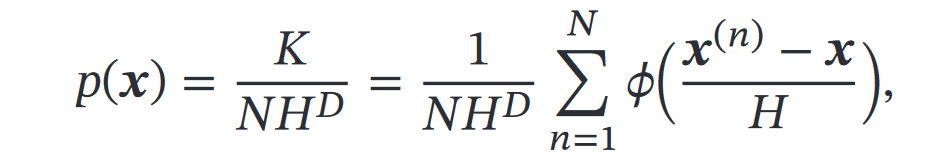
高斯核函数


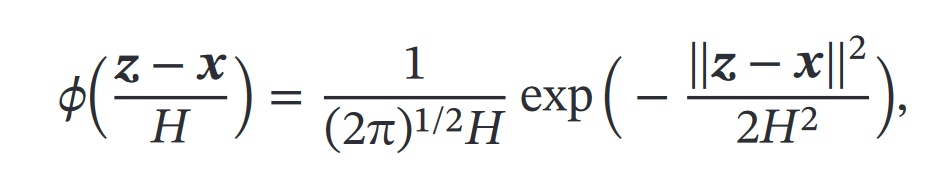然后就得到了：

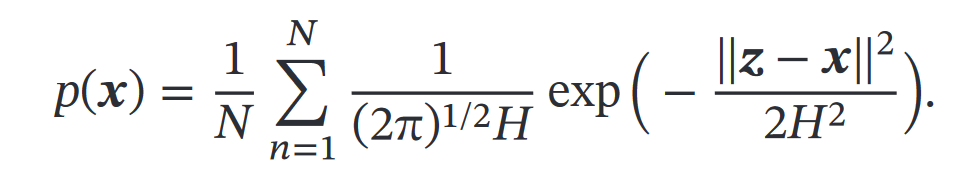
⑤K近邻方法（KNN）

KNN用于分类已经很熟悉了

在密度估计上，KNN是这么做的：

设置可变宽度区域，使落入每个区域样本数量都是为固定数量K个

然后我们在估计某点的密度时，找到以这个点为中心的球体，这个球体的大小使得落入球体的样本数量也是K个。

从而我们得到了V，而N是训练样本数量已知，K我们预先设定。

然后根据𝑝(𝒙)≈ 𝐾/𝑁𝑉就可以了。

第10章 模型独立的学习方式

> 模型独立：学习方式不限于具体模型（但是也会因模型特性不同而有不同程度的效果） >

一、集成学习

1.思想


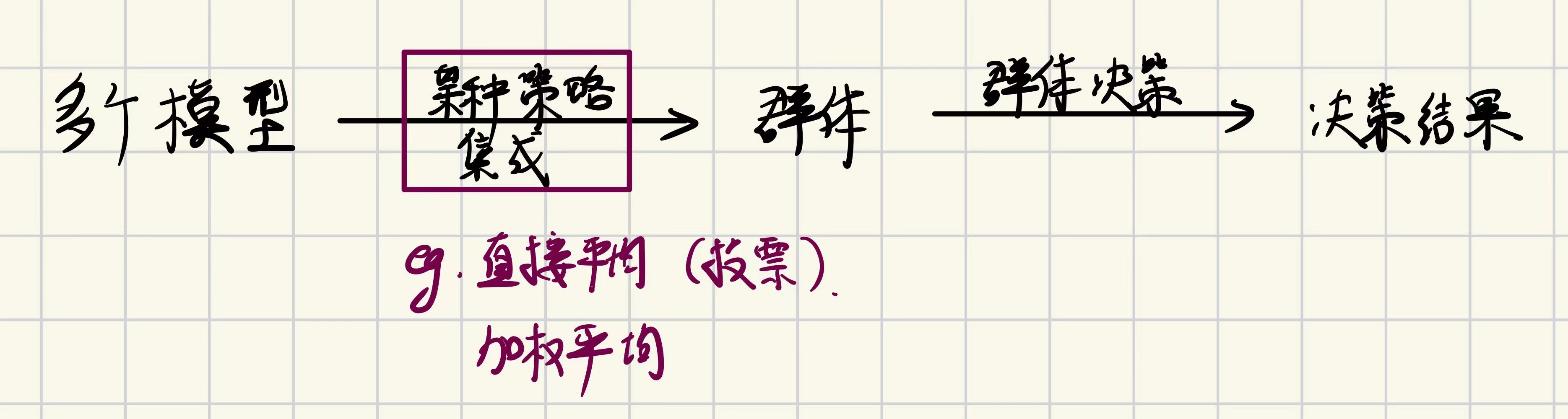“三个臭皮匠赛过诸葛亮”的同时，需要每个基模型差异尽可能大（和而不同）

=> 使差异大的方式：Bagging类方法，Boosting类方法

2.Bagging类方法

（1）思想

引入随机性：随机构造训练样本/随机选择特征

（2）Bagging——随机构造训练样本

在原始数据集上进行有放回的随机采样，得到M个小训练集，训练M个模型，然后投票

（3）随机森林——Bagging+随机选择特征

每个基模型都是一颗决策树

3.Boosting类方法

（1）思想

每个基模型针对**前序模型的错误**进行专门训练

=>前序模型发生错误的训练样本的权重，调高！反之，调低！

（2）目标

学习一个加性模型：`加性模型 = 从1到M求和（第m个基分类器的集成权重 * 第m个基分类器）`

                                          （基分类器=弱分类器）

（3）AdaBoost算法

①思想

通过**改变数据分布**来提高分类器的差异，迭代训练

=>每轮训练增加分错样本的权重，减少分对样本的权重

②算法

* 根据第`m`轮的样本权重，学习第`m`个分类器`𝑓<sub>𝑚</sub>` * 计算`𝜖<sub>𝑚</sub>`，`𝜖<sub>𝑚</sub>`是弱分类器`𝑓<sub>𝑚</sub>`在数据集上的加权错误 * 计算`𝛼<sub>𝑚</sub>`，`𝛼<sub>𝑚</sub>`是第`𝑚`个分类器在集成时的权重，`𝛼<sub>𝑚</sub> ← 1/2 * log (1 −𝜖<sub>𝑚</sub>/𝜖<sub>𝑚</sub>)` * 调整样本权重，`𝑤<sup>(𝑛)</sup> <sub>𝑚+1</sub> ← 𝑤<sup>(𝑛)</sup> <sub>𝑚</sub> exp ( − 𝛼<sub>𝑚</sub>𝑦<sup>(𝑛)</sup>𝑓<sub>𝑚</sub>(𝒙<sup>(𝑛)</sup>)), ∀𝑛 ∈ [1, 𝑁]` * 根据第`m+1`轮的样本权重，学习第`m+1`个分类器`𝑓<sub>𝑚+1</sub>` * 。。。。。。。

（4）《机器学习方法》中关于Boosting的内容

[第8章 Boosting](https://www.yuque.com/yuqueyonghucoit3e/wefx9h/lu10ii76mdplhi4g)

二、自训练和协同训练——半监督学习算法

0.半监督学习

少量标注数据 + 大量无标注数据 --> 进行学习

1.自训练/自举法

（1）思想

有标注的数据——训练模型——模型预测无标住样本标签——预测置信度高的样本+模型预测的无标注样本的标签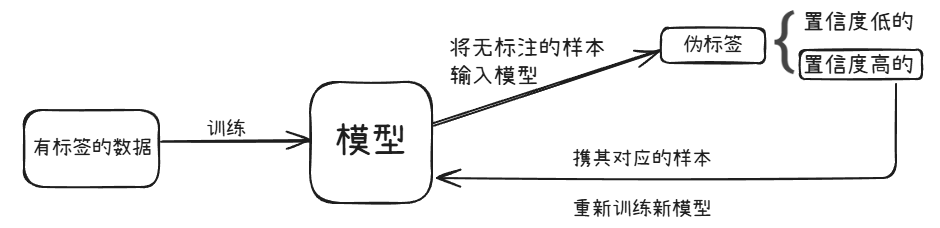

（2）缺点

无法保证伪标签是正确的——if伪标签是错的，反而会损害模型预测能力

2.协同训练——自训练的一种改进方法

:::info **视角**的概念： 数据的不同侧面

eg.每个网页的类别，可以从文字内容判断（视角V₁），也可以根据网页间链接关系判断（视角V₂）

:::

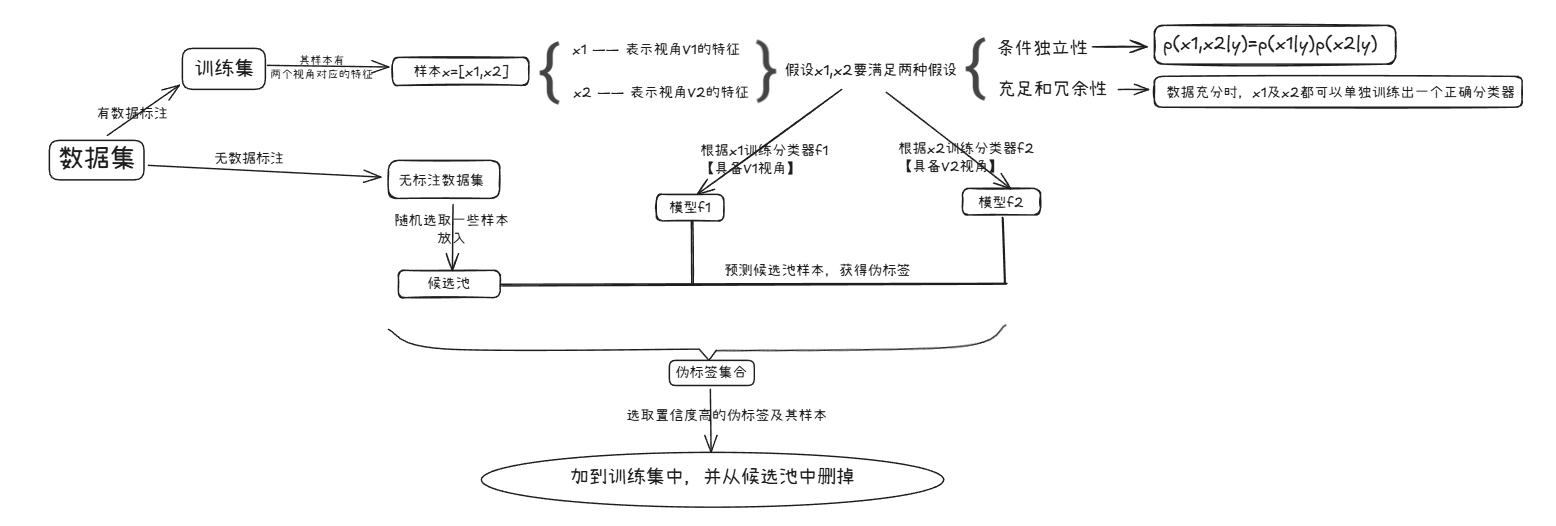
训练出的模型f1，f2具备两个不同的视角，具有一定的互补性

三、多任务学习

1.思想

**同时**学习多个**相关任务**，学习过程中**共享知识**，利用**任务间相关性**来改进模型在每个任务上的性能和泛化能力

可看做一种归纳迁移学习——利用包含在相关任务中的信息，作为归纳偏置，以提高泛化能力

2.常见的4种共享机制

（1）硬共享模式

不同任务的NN模型共用一些共享模块（**通常低层**）来提取**通用特征**

不同任务再设置私有模块（通常高层）来提取任务特定特征

（2）软共享模式

不显式共享，而是允许每个任务从其他任务中**窃取**信息来提高自己的能力

=>窃取方式：

①直接复制使用其他任务的隐状态

②使用Attention机制主动选取有用的信息

（3）层次共享模式

:::info 神经网络**不同层抽取的特征类型**：

低层——低级的局部特征

高层——高级的抽象语义特征

:::

根据多任务学习中不同任务级别高低：

低级任务在低层输出

高级任务在高层输出

（4）共享-私有模式

共享模块和任务特定（私有）模块分开

共享模块——捕捉跨任务共享特征

私有模块——捕捉特定任务相关特征

3.学习步骤

（1）联合训练阶段

①随机初始化模型参数

②1······T轮迭代开始进行

③把每一个任务的训练集都随即划分小批量集合，划分数量𝑐 = 𝑁<sub>𝑚</sub>/𝐾<sub>𝑚</sub>

𝑁<sub>𝑚</sub>为第𝑚个任务的训练集包含的样本数量

𝐾<sub>𝑚</sub>为第𝑚个任务的批量大小

④合并所有小批量样本，并随机排序打乱

⑤计算合并后的集合中，每个小批量样本上的损失，并更新参数

⑥继续迭代，直到结束，输出𝑚个模型

（2）单任务精调阶段

刚才得到了参数，基于这些参数，在每个单独任务进行精调

3.相较单任务学习泛化能力更好的原因

（1）训练集更大（毕竟是多任务）

（2）任务间有相关性（相当于隐式的数据增强）

（3）避免过拟合到单个任务的训练集（共享需兼顾所有任务【相当于一种正则化】）

（4）获得了更好的表示（适用于多个不同任务）

（5）可选择性利用其他任务学习到的隐藏特征

四、迁移学习

1.基础概念

（1）领域`𝒟 = (𝒳, 𝒴, 𝑝(𝒙, 𝑦))`

①领域

一个样本空间及其分布

②源领域`𝒟<sub>𝑆</sub>`

③目标领域`𝒟<sub>𝑇</sub>`

④领域间关系

* 不同领域：输入空间不同 或 输出空间不同 或 概率分布不同 * 源领域的样本数量一般远大于目标领域

2.思想

将相关任务的训练数据中的可泛化知识迁移到目标任务上

（利用源领域中学习的知识来帮助目标领域上的任务）

3.归纳迁移学习与转导迁移学习

（1）归纳学习与转导学习

归纳学习：最小化期望风险得到模型，一般的机器学习就是归纳学习

转导学习：最小化给定测试集上的错误率，训练阶段可利用测试集信息

（2）归纳迁移学习

①思想

源领域及其任务 --> 学习出一般规律 -->迁移到目标领域及其任务上

②要求

a.源领域和目标领域相关

b.源领域有大量训练样本（可以有标注可以无标注）

+ 源领域有大量无标注数据时：

源任务

–> 转换为无监督学习任务（eg.自编码/密度估计）

–> 学习出可迁移表示

–> 迁移到目标任务

        + 源领域有大量有标注数据时：

源任务

–> 学习训练出模型

–> 模型迁移到目标领域目标任务上

③两种迁移方式

a.基于特征的方式

预训练模型的输出/中间隐藏层的输出 --> 作为特征 --> 直接加入到目标任务的学习模型中

b.精调的方式

在目标任务上复用预训练模型的部分组件，并对其参数进行精调

有针对性地选择预训练模型的不同层迁移到目标任务中

④预训练模型迁移的优点（相较于从零开始学习）

a.初始模型性能比随机初始化的模型好

b.训练时模型的学习速度比从零开始学习快

c.模型最终性能更好，泛化性更好

⑤与多任务学习的区别

a.多任务学习是同时学习多个任务，归纳迁移学习是分两个阶段的

（源任务上的学习阶段+目标任务上的迁移学习阶段）

b.多任务学习希望提高所有任务的性能，归纳迁移学习是单向知识迁移、只针对目标任务

（3）转导迁移学习

①思想

直接利用源领域和目标领域的样本进行迁移学习

②常见子问题——领域适应

a.什么是领域适应问题

假设源领域和目标领域有相同的样本空间，但**数据分布不同**

b.数据分布不一致的情况

+ 协变量偏移：两领域输入边际分布不同，但后验分布（即学习任务）相同 + 概念偏移：两领域输入边际分布相同，但后验分布（即学习任务）不同 + 先验偏移：两领域中输出标签的先验分布不同，条件分布相同

:::info
协变量的概念：

可能影响预测结果的统计变量

机器学习中，可以看作输入

协变量偏移的概念：

输入在训练集和测试集上的分布不同

:::

c.领域适应问题要做什么

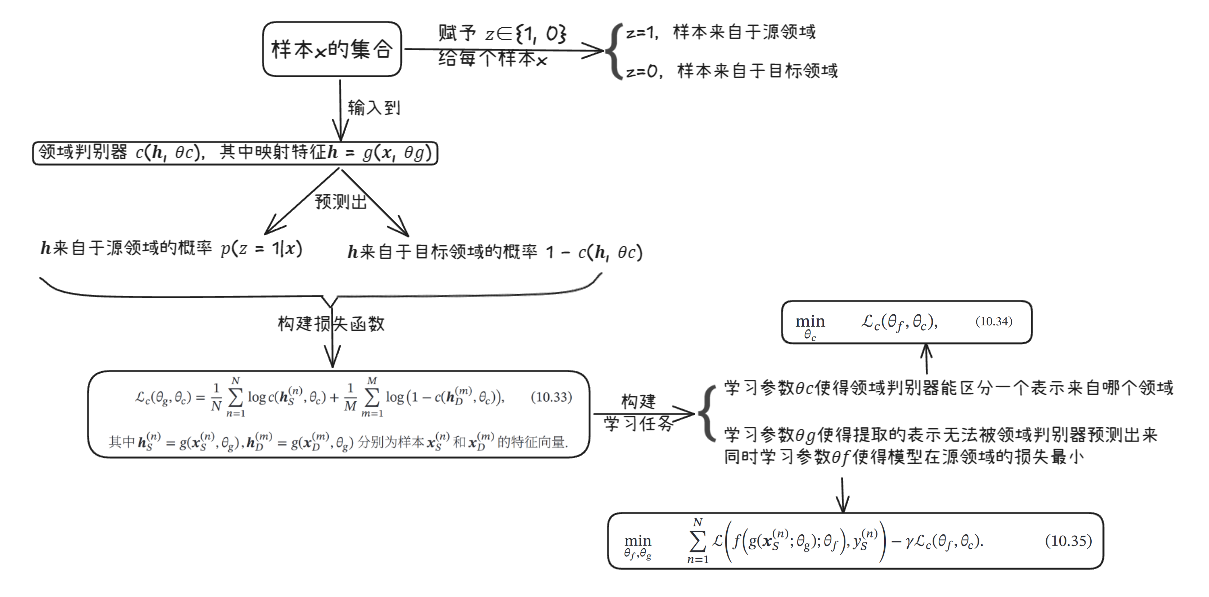
关键在于如何学习领域无关的表示！

d.如何学习领域无关的表示

+ 优化参数使得映射后的两个领域的输入分布差异最小

        + 通过领域对抗学习

引入领域判别器𝑐来判断一个样本是来自于哪个领域

if 𝑐 不能判断一个映射特征的领域信息，则是一个领域无关的表示

具体做法见下图

五、终身学习/持续学习

> 像人类一样具有持续不断的学习能力，不因新知识忘记旧知识，反而用旧知识帮助学习新知识 >

1.终身学习和其他学习的比较

（1）终身学习vs归纳迁移学习

归纳迁移学习只关注优化目标任务性能，不关注知识的积累

终身学习目标是持续的学习和知识积累

（2）终身学习vs多任务学习

多任务学习在所有任务上同时进行联合学习

终身学习是持续的一个一个学习

2.关键问题——如何避免灾难性遗忘

目前神经网络往往过参数化 --> 一个任务有很多参数组合都可达到最好性能 --> 选择一组不影响先前任务的参数

一个方法——弹性权重巩固

以两个任务的持续学习为例子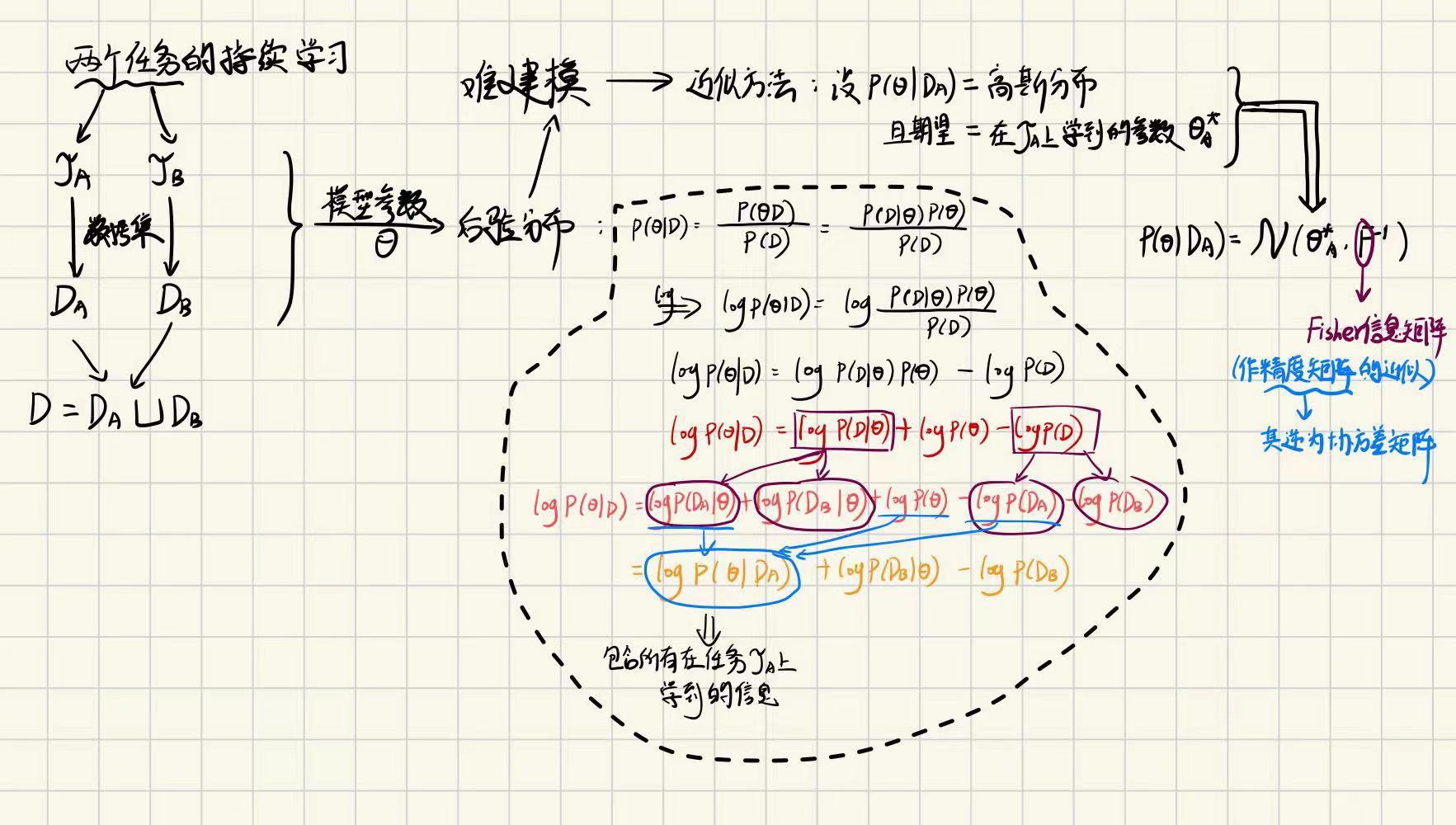

①对Fisher信息矩阵部分进一步说明逻辑

我们用Fisher信息矩阵近似精度矩阵，是因为精度矩阵与协方差矩阵存在互为逆矩阵的关系。

本质上想要的是协方差矩阵。

同时Fisher信息矩阵可以简化为对角矩阵，由Fisher信息矩阵对角线构成。

②那么什么是Fisher信息矩阵呢

性质：一种测量似然函数`𝑝(𝑥;𝜃)`携带的关于参数`𝜃`的信息量的方法

怎么得出的：首先，有一个通常的事实——一个参数对分布的影响，可以通过对数似然函数的梯度衡量

然后，我们就让设计一个打分函数𝑠(𝜃)以符合这个事实，即𝑠(𝜃) = ∇<sub>𝜃 </sub>log 𝑝(𝑥; 𝜃)

其中，这个函数有个性质，是期望为0，证明略

最后，这个函数的协方差矩阵，就是Fisher信息矩阵，可以衡量参数𝜃的估计的不确定性

也就是：𝐹(𝜃) = 𝔼[𝑠(𝜃)𝑠(𝜃)<sup>T</sup>]= 𝔼 [∇<sub>𝜃</sub> log 𝑝(𝑥; 𝜃) (∇<sub>𝜃</sub> log 𝑝(𝑥; 𝜃))<sup>T</sup>]

（解释一下，这里就是在算协方差，Cov=E[s²]-(E[s])²，又因为期望为0，所以只剩前面那项）

得到之后的问题：对于𝐹(𝜃)表达式，其中的似然函数𝑝(𝑥;𝜃)我们不知道具体形式，咋办呢？

可用经验分布估计：

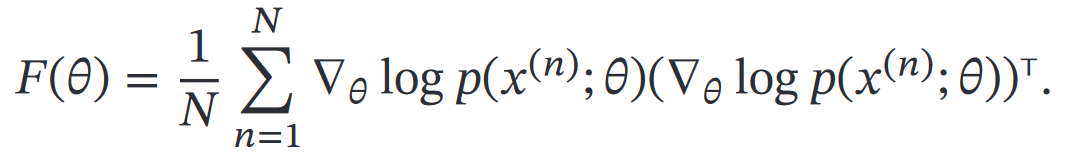
然后怎么用：一方面，𝐹(𝜃)对角线的值反应𝜃在通过最大似然进行估计时的不确定性

–>值大：则估计值方差越小，估计越可靠，携带关于数据分布的信息越多

–>值小：则估计值方差越大，估计越不可靠，携带关于数据分布的信息越少

另一方面，可用作信息量的衡量，用下面这个公式来衡量

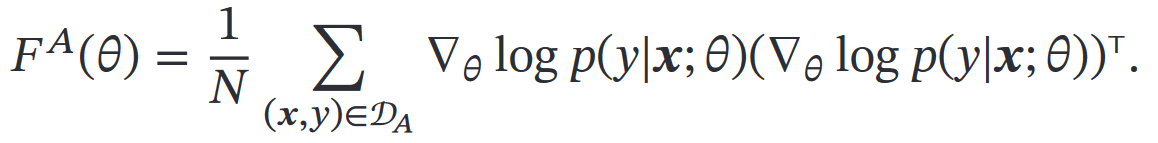
还有，得到了训练任务𝒯<sub>𝐵</sub>时的损失函数

六、元学习——学习的学习

> 动态调整学习方式，像人脑一样，面对不同任务，自动找到对应的解决方式 >

1.目的

从已有任务中，学习一种学习方法或元知识，从而可以加速新任务的学习

2.与归纳迁移学习的区别

元学习更侧重从多种不同，甚至不相关的任务中，归纳出一种学习方法

而归纳迁移学习有相关性要求，即要求源领域和目标领域相关

3.和元学习比较相关的机器学习问题——小样本学习

每个类只有K个标住样本，其中K非常小

if K=1，称为单样本学习

if K=0，称为零样本学习

4.典型的元学习方法

（1）基于优化器的元学习


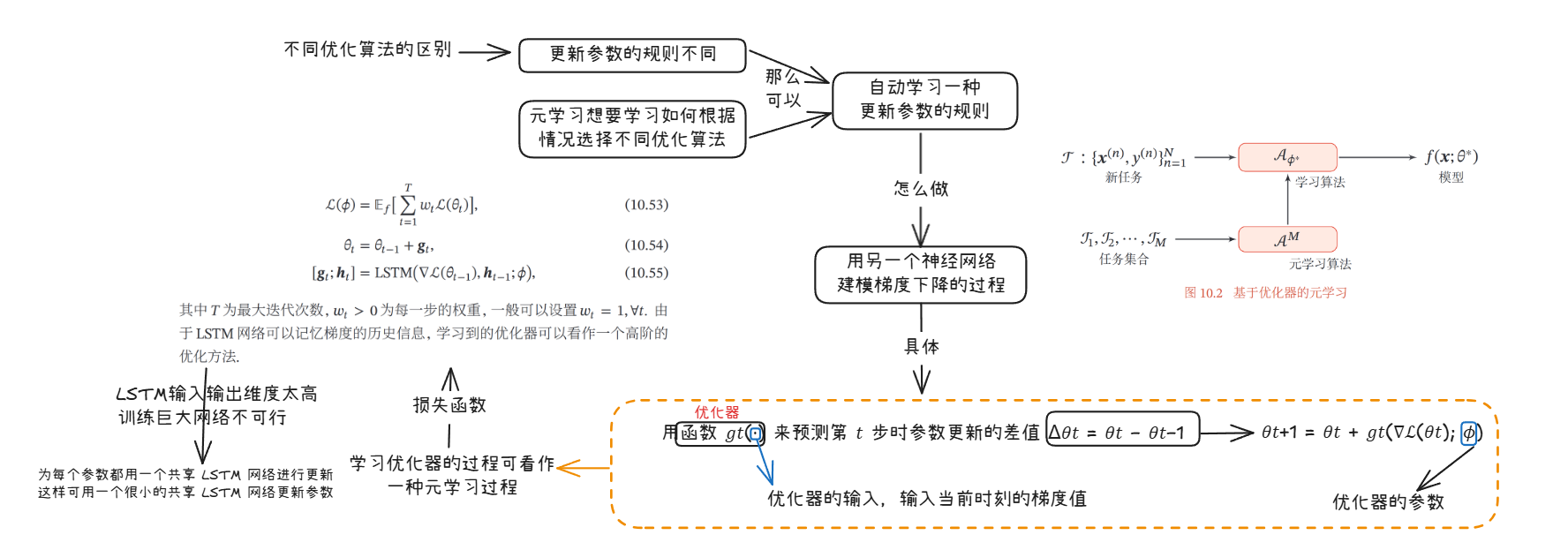（2）模型无关的元学习 MAML

①做法

假设所有任务来自共同的一个任务空间

–> 利用这些任务学习一个通用表示（称为在所有任务上的元优化，也采用梯度下降进行优化，得到θ）

–> 在特定单任务上，通过梯度下降来精调θ

②目标

学习一个参数θ，这个θ经过梯度迭代，就可以在新任务上达到最好性能

③算法

可以看一下，其实和前面说的做法是一致的

第11章 概率图模型

> 用图结构来描述多元随机变量间条件独立关系的概率模型 >

问题的导出

:::info K维随机变量——联合概率为高维空间分布——难建模——需要参数量简直爆炸——怎么减少参数量

为了减少参数量——做独立性假设——𝑝(𝒙) ≜ 𝑃(𝑿 = 𝒙) = ∏ 𝑝(𝑥<sub>𝑘</sub>|𝑥<sub>1</sub>, ⋯ , 𝑥<sub>𝑘−1</sub>)连乘起来

连乘的是每个分开的条件概率——通过条件依赖关系大大减少参数量

但变量数量太多时条件依赖关系复杂——图结构可视化概率模型

——描述条件独立性+复杂联合概率模型分解为简单条件概率模型的组合

:::

1.图模型的三个基本问题

表示问题：如何用图结构描述变量间依赖关系

学习问题：（图结构的学习）和参数学习

推断问题：已知部分变量，计算其他变量条件概率分布

2.图模型与机器学习非关系

很多机器学习模型可归结为概率模型

二、模型表示

1.要素

节点：一组/一个随机变量

边：随机变量间的概率依赖关系

2.分类

有向图模型

* 有向非循环图 * 有连边——两变量有因果关系——不存在其他随机变量使得这俩变量条件独立

无向图模型

* 无向图 * 有连边——两变量有概率依赖关系，不一定因果关系

3.有向图模型=贝叶斯网络=信念网络

（1）两个节点直接连接

它们必然非条件独立，且是直接因果关系——父节点是因，子结点是果

（2）两个节点不直接连接，但经过其他节点可达

①间接因果关系

②间接果因关系

③共因关系：因X₂已知，则独立

④共果关系：果X₂已知，则不独立

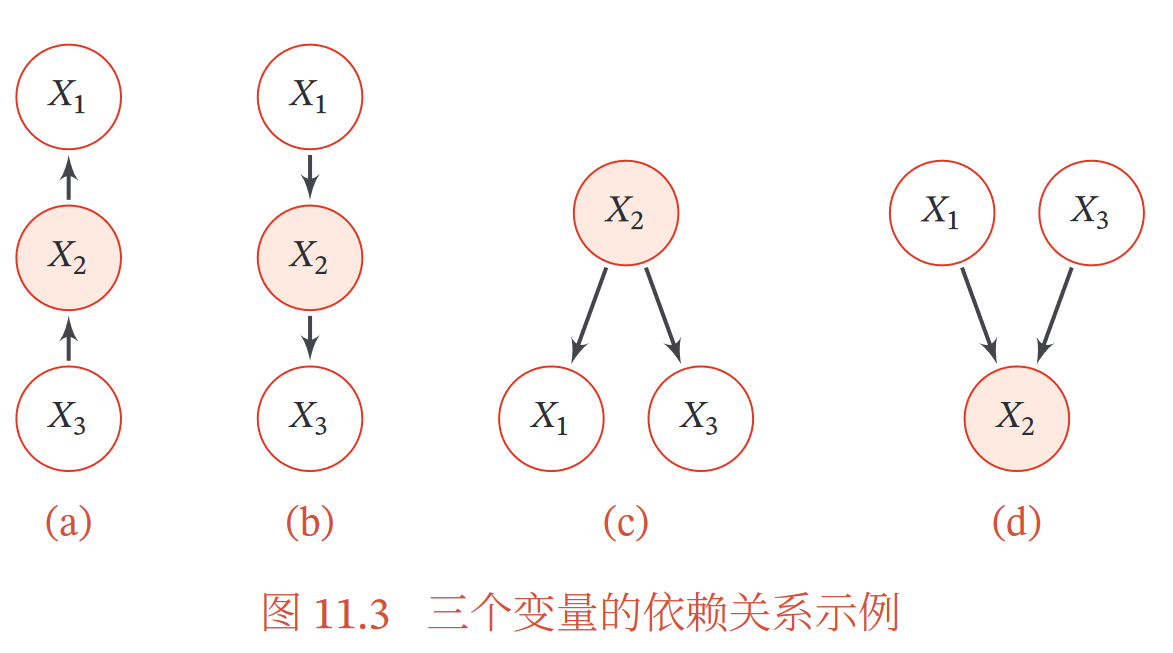
参照这张图来理解，其中x₂是中间节点

（3）局部马尔可夫性

给定父节点，则每个随机变量要条件独立于它的非后代节点

    * 后代节点可以有关系
    * 但是非后代节点得条件独立

（4）常见的有向图模型

①Sigmoid信念网络（SBN）


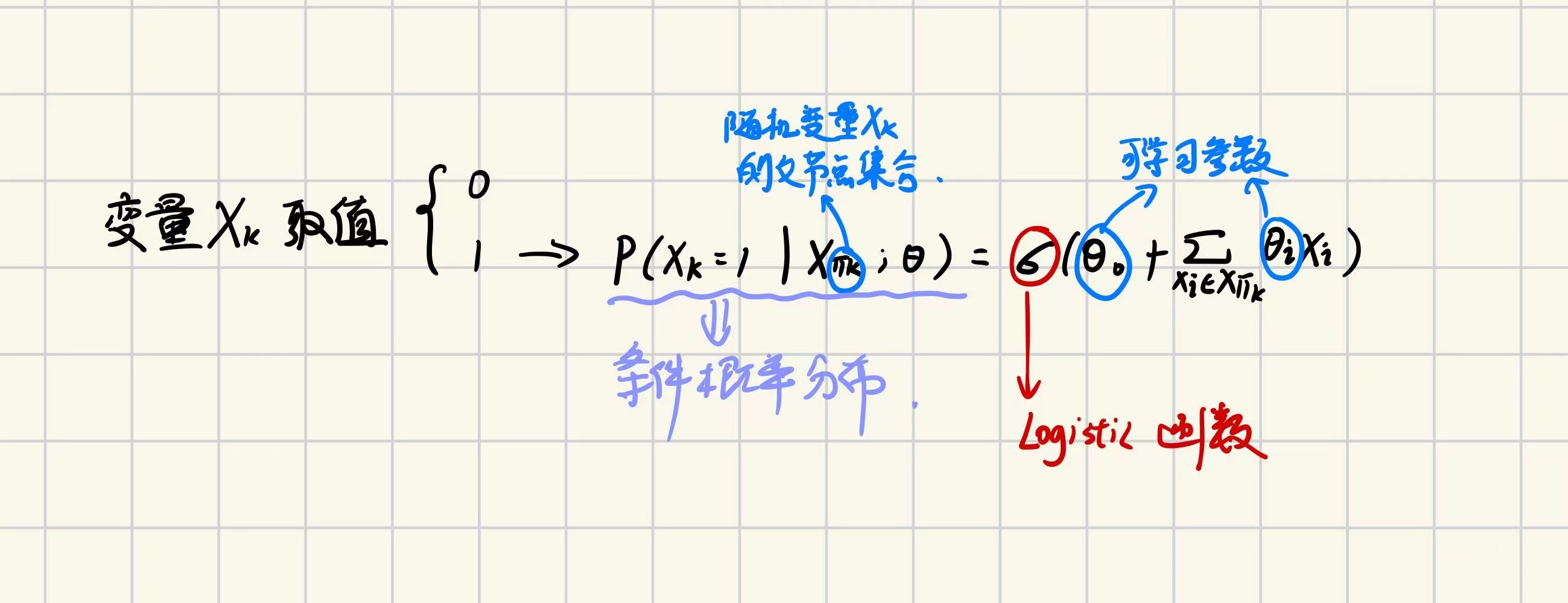与Logistic回归模型的区别：

        + **𝒙**的本质：Logistic回归模型的**𝒙**是确定性参数而不是变量

Sigmoid信念网络的𝒙是随机变量

        + 模型本质：Logistic 回归模型只建模条件概率 𝑝(𝑦|𝒙)，是一种**判别模型**

      Sigmoid信念网络建模联合概率 𝑝(𝒙, 𝑦)，是一种**生成模型**

②朴素贝叶斯分类器（NB）

原理：贝叶斯公式+强独立性假设（朴素所在）---> 计算每个类别条件概率

𝑝(𝑦|𝒙;𝜃) ∝ 𝑝(𝑦|𝜃<sub>𝑐</sub>) ∏ 𝑝(<font style="color:#DF2A3F;">𝑥</font><sub><font style="color:#DF2A3F;">𝑚</font></sub>|𝑦;𝜃<sub>𝑚</sub>)

若<font style="color:#DF2A3F;">𝑥</font><sub><font style="color:#DF2A3F;">𝑚</font></sub>是连续值——可用高斯分布建模

若<font style="color:#DF2A3F;">𝑥</font><sub><font style="color:#DF2A3F;">𝑚</font></sub>是连续值——可用多项式分布建模

③隐马尔可夫模型（HMM）

所有隐变量构成一个马尔可夫链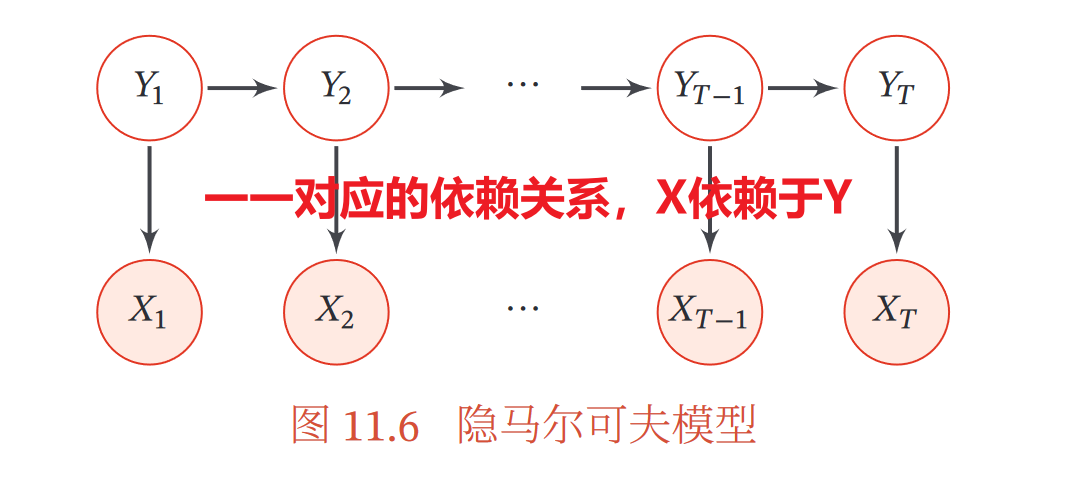

𝑝(𝒙, 𝒚;𝜃) = ∏ 𝑝(𝑦<sub>𝑡</sub>|𝑦<sub>𝑡−1</sub>, 𝜃<sub>𝑠</sub>) 𝑝(𝑥<sub>𝑡</sub>|𝑦<sub>𝑡</sub>, 𝜃<sub>𝑡</sub>)

转移概率 输出概率

《机器学习方法》中关于隐马尔可夫模型的内容：

第10章 隐马尔可夫模型

4.无向图模型=马尔可夫随机场=马尔可夫网络

（1）定义

用无向图来描述一组具有局部马尔可夫性质的随机向量 𝑿 的联合概率分布的模型

（也就是具备局部马尔可夫性的无向图）

（2）无向图的局部马尔可夫性

𝑋_𝑘 条件独立于 除了自己和邻居 以外的 所有节点

（3）无向图模型的概率分解

①团

无向图中的一个全连通子图——所有节点都有边相连 所形成的一坨

②最大团

不能被其他团包含了 就是最大团

当然 如果再加一个节点就不满足全连通性 也就是最大团

③因子分解

分布`𝑝(𝒙) > 0`满足无向图中的局部马尔可夫性

=>𝑝(𝒙)可表示为𝑝(𝒙) = 1/𝑍 ∏ 𝜙<sub>𝑐</sub>(𝒙<sub>𝑐</sub>) ——吉布斯分布

            - `𝜙<sub>𝑐</sub>(𝒙<sub>𝑐</sub>) ≥ 0 `是定义在团 𝑐 上的势能函数
            - 配分函数 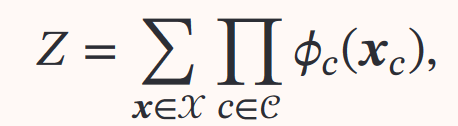![](https://cdn.nlark.com/yuque/0/2024/png/40781129/1732186231573-da14ef8a-40ec-4415-b16a-3d5cfae46907.png) 用来归一化乘积为概率形式

④吉布斯分布

`𝑝(𝒙) = 1/𝑍 ∏ 𝜙<sub>𝑐</sub>(𝒙<sub>𝑐</sub>)` ，其中一般定义`𝜙<sub>𝑐</sub>(𝒙<sub>𝑐</sub>) = exp(−𝐸<sub>𝑐</sub>(𝒙<sub>𝑐</sub>))`且`𝐸<sub>𝑐</sub>(𝒙<sub>𝑐</sub>)` 为能量函数

这个形式称为吉布斯分布                                              这样定义后，分布又称为玻尔兹曼分布

性质是：吉布斯分布一定满足马尔科夫随机场条件独立性质

马尔科夫随机场的概率分布一定可以表示成吉布斯分布

（4）常见的无向图模型

①对数线性模型=条件最大熵模型=Softmax回归模型

刚才提到的吉布斯分布`𝑝(𝒙) = 1/𝑍 ∏ 𝜙<sub>𝑐</sub>(𝒙<sub>𝑐</sub>)` ，让其中的`𝜙<sub>𝑐</sub>(𝒙<sub>𝑐</sub>)`为：

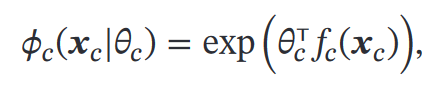
然后取对数：

𝑓<sub>𝑐</sub>(𝒙<sub>𝑐</sub>) 为定义在 𝒙<sub>𝑐</sub> 上的特征向量；𝜃<sub>𝑐</sub> 为权重向量

然后得到 𝑝(𝑦|𝒙;𝜃)：

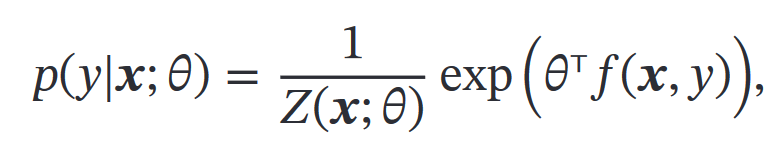
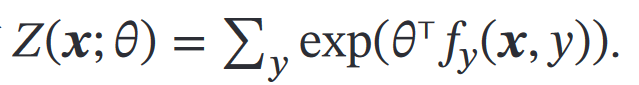
《机器学习方法》中关于最大熵模型的内容：

第6章 逻辑斯谛回归与最大熵模型

②条件随机场

对y要有分解，即：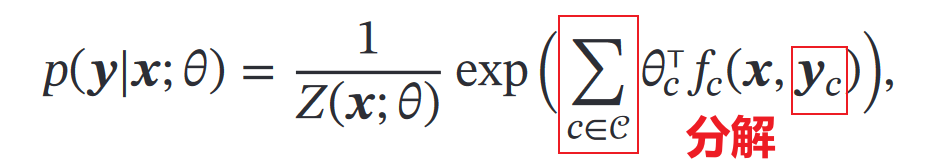

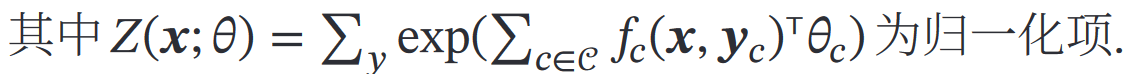
（可以对比最大熵模型的条件概率公式，可以发现做了分解）

线性链条件随机场的条件概率：

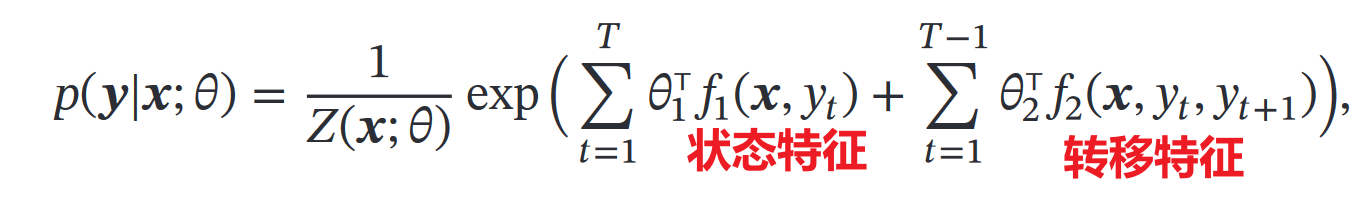
《机器学习方法》中关于条件随机场的内容：

第11章 条件随机场

③玻尔兹曼机

见第12章

④受限玻尔兹曼机

见第12章

（5）有向图和无向图间的转换

①为啥

有向图转无向图，可以利用无向图上的精确推断算法，同时也可以表示有向图无法表示的一些**依赖关系**

（注意不是所有关系，比如无向图是不能表示因果关系的）

②过程--道德化

看图理解就行：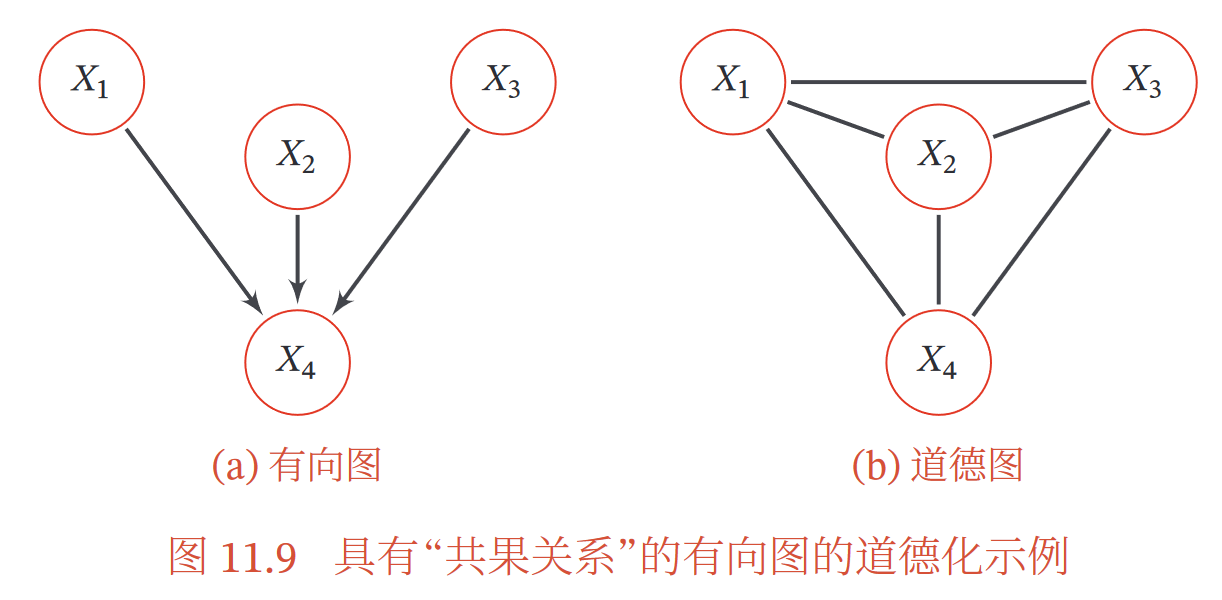

三、模型的学习

1.分类

寻找最优网络结构（难，专家构建）+ 已知网络结构估计每个条件概率分布参数（按包不包含隐变量分两种）

2.不含隐变量的参数估计——最大似然

（1）有向图模型

①第一步，构造对数似然


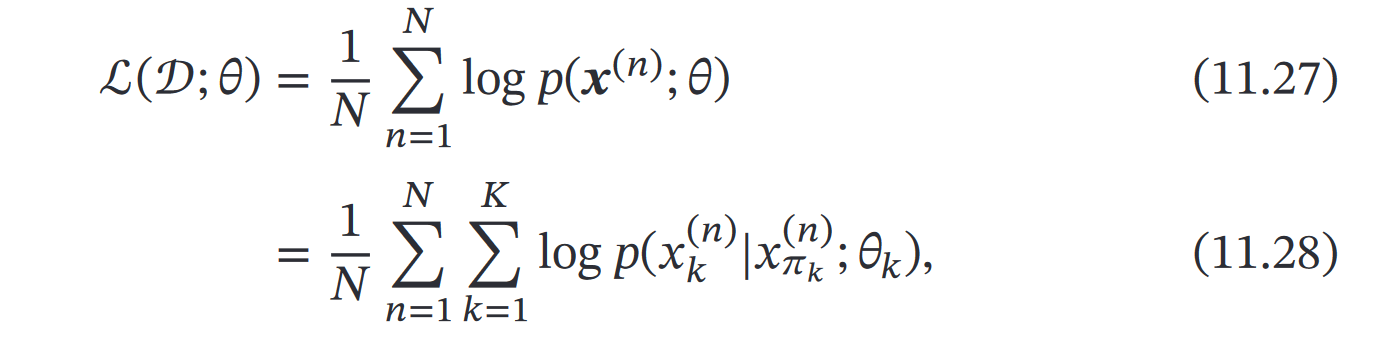从11.27到11.28，是因为：

”所有变量 𝒙 的联合概率分布可分解为每个随机变量 𝑥_𝑘 的局部条件概率 𝑝(𝑥_𝑘|𝑥_𝜋𝑘 ; 𝜃_𝑘) 的连乘形式“

说人话就是：

可以拆成部分连乘形式，然后log一下，就变成了累加~

②第二步，最大化对数似然`ℒ(𝒟; 𝜃)`

转化为分别最大化每个变量的条件似然，即：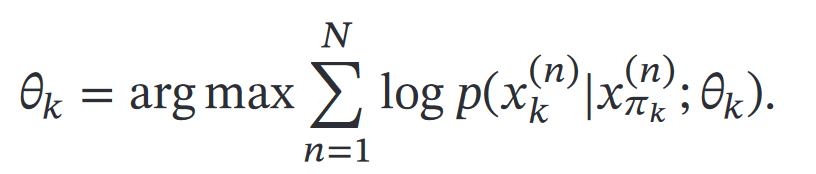

    * 如果x离散——使用参数化模型减少参数量——例如用Sigmoid信念网络
    * 如果x连续——用高斯函数表示条件概率分布——高斯信念网络

（2）无向图模型

①第一步，构造对数似然


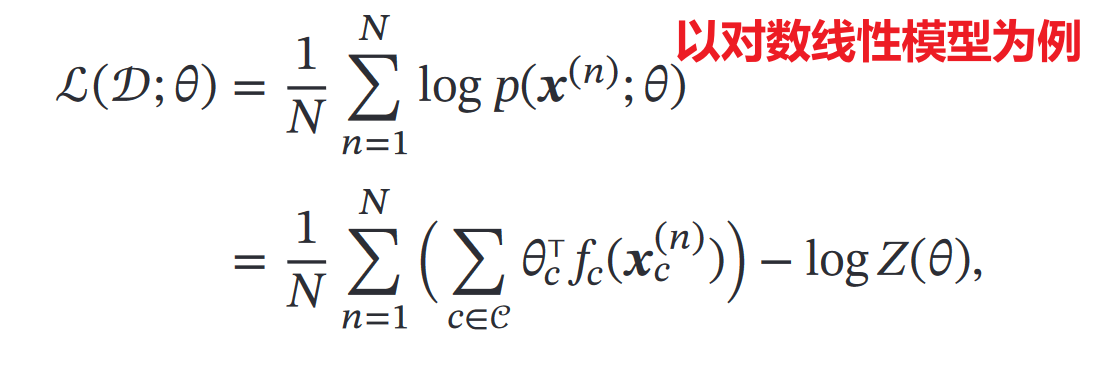这里直接就代入了对数线性模型的概率公式：

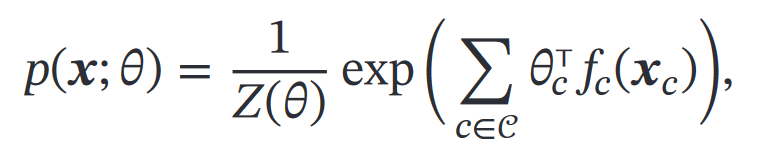
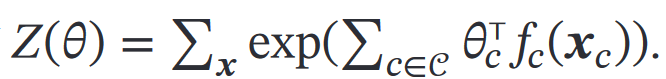
②第二步，最大化对数似然`ℒ(𝒟; 𝜃)`

用梯度上升方法：

求关于𝜃_𝑐 的偏导数，推导过程如下

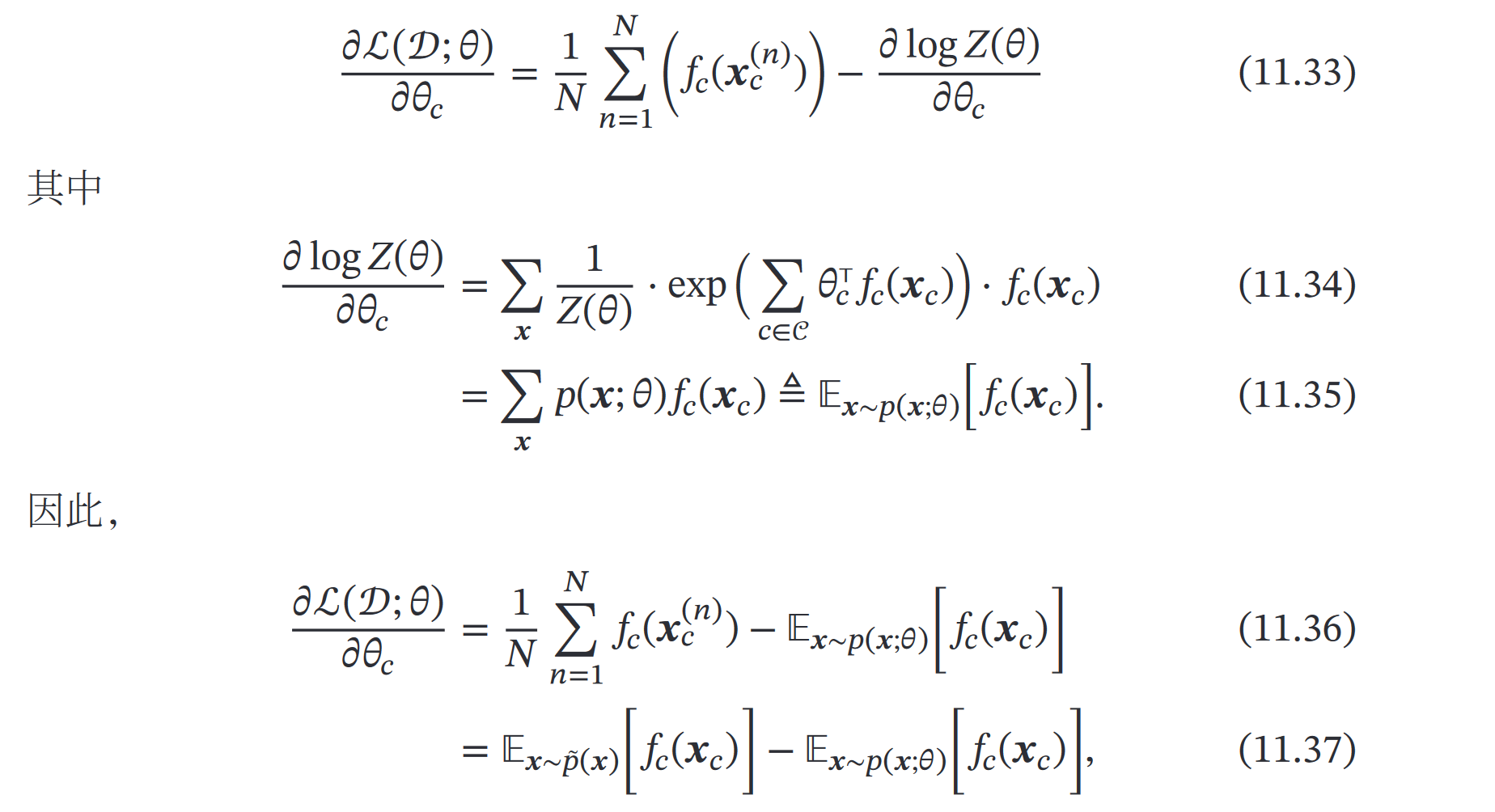
最优点梯度为0，也就是式11.37等于0，从而也就是书上说的“优化目标等价于：对于每个团 𝑐 上的特征 𝑓_𝑐(𝒙_𝑐)，使得其在经验分布 ̃𝑝(𝒙) 下的期望等于其在模型分布 𝑝(𝒙; 𝜃) 下的期望”

式11.37的后半部分（在模型分布下的期望）很难算，通常采用近似，有两种方式：

a.利用采样来近似计算期望

b.坐标上升法：固定其他参数，优化一个势能函数的参数

3.含隐变量的参数估计

（1）EM算法

> 这里同样也是从最大化对数似然的原理出发得到的EM算法 >

逻辑：首先我们有一个样本 𝒙 的边际似然函数（i.e.证据）

然后构造对数似然，和前面”不含隐变量的参数估计“部分的公式原理相同，长下面这样

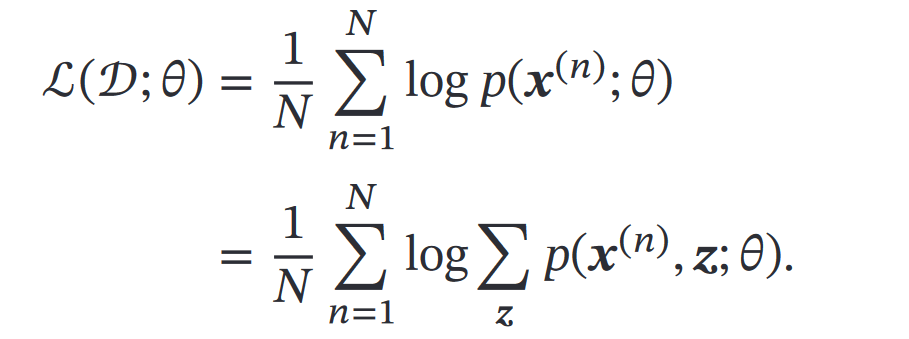
然后我们要最大化对数似然，但涉及到 𝑝(𝑥) 的推断问题（导致对数函数内部的求和/积分去不掉且难算）

然后我们就引入变分函数𝑞(𝒛)（定义在隐变量 𝒁 上的分布）来解决问题，得到下面这样

![](https://cdn.nlark.com/yuque/0/2024/png/40781129/1732453192935-083b22ef-2d25-4118-891e-48487015a778.png)

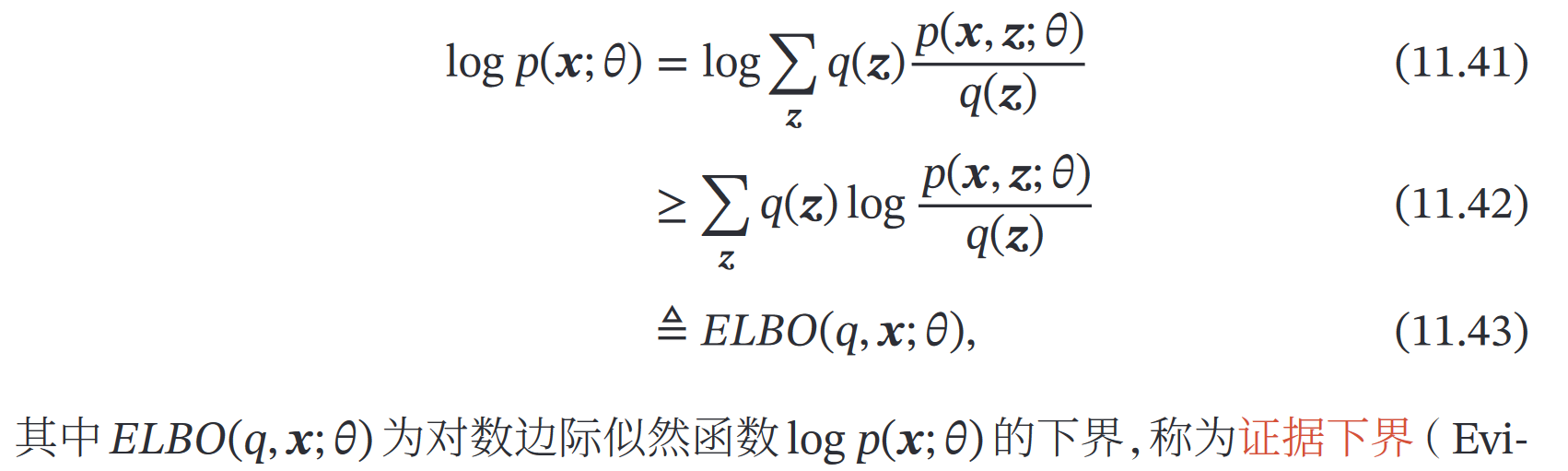
所以最大化似然函数就转化为了两步的不断重复直到收敛到局部最优解：

①E步

固定参数 𝜃_𝑡，找到一个分布 𝑞_𝑡+1(𝒛) 使得证据下界 𝐸𝐿𝐵𝑂(𝑞, 𝒙; 𝜃_𝑡) 等于 log 𝑝(𝒙; 𝜃_𝑡)

其中，最理想有𝑞(𝒛) = 𝑝(𝒛|𝒙,𝜃<sub>𝑡</sub>)，因为此时𝐸𝐿𝐵𝑂(𝑞<sub>𝑡+1</sub>, 𝒙; 𝜃)最大

但是，如果𝒛的维度较高，𝑝(𝒛|𝒙,𝜃<sub>𝑡</sub>)不好算，需要变分推断方法

②M步

固定 𝑞_𝑡+1(𝒛)，找到一组参数使得证据下界最大

𝜃<sub>𝑡+1</sub> = arg max <sub>𝜃</sub> 𝐸𝐿𝐵𝑂(𝑞<sub>𝑡+1</sub>, 𝒙; 𝜃)

收敛性证明略

信息论视角推导出EM算法略

《机器学习方法》中关于EM算法的内容：

第9章 EM算法及其推广

四、模型的推断

1.推断

（1）概念

观测到部分变量时，计算其他变量的某个子集的条件概率

=>关键在：求任意一个变量子集的边际分布

（2）分类

精确推断、近似推断

2.精确推断

（1）变量消除法

`p(x<sub>1</sub>|x<sub>4</sub>)=p(x<sub>1</sub> , x<sub>4</sub>) / p(x<sub>4</sub>)`

其中：

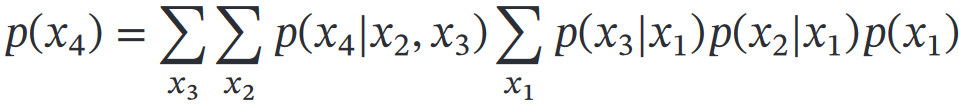
这个过程中消除了变量，减少计算边际分布的计算复杂度

（2）信念传播算法=BP算法=和积算法=消息传递算法

思想：将变量消除法的和积操作看作消息并保存

消息传递过程：

树结构上的信念传播算法


3.近似推断

if图模型结构复杂=>精确推断开销大

if图模型变量连续+积分函数没有闭式解=>无法使用精确推断

（1）环路信念传播

在具有环路的图上用信念传播算法

（2）变分推断

引入简单分布（称为变分分布）近似条件概率，迭代计算：

更新变分分布参数，最小化变分分布和真实分布的差异=>根据变分分布来推断

（3）采样法

用模拟方式采集符合某个分布的样本，用样本估计和分布有关的运算

五、变分推断

泛函：函数的函数，输入是函数，输出是实数=> f(x)的泛函：F(f(x))

变分法：寻找使F(f(x))取得极大/极小值的f(x)

变分推断：推断问题转换为泛函优化问题——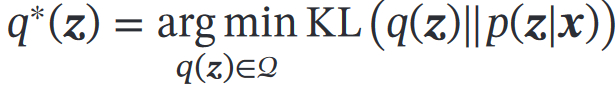最小化变分分布和真实分布差异

这个问题的解法：

六、基于采样法的近似推断

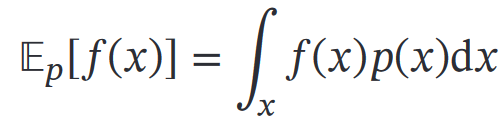 其中要推断的概率分布为p(x)，采样法近似计算这个期望

1.采样法=蒙特卡罗方法=统计模拟方法

通过随机采样（给定概率密度函数中抽取符合其概率分布的样本）近似估计计算问题数值解

过程：p(x)中独立抽取N个样本 => N个样本的均值近似为f(x)的期望 => N无穷大时收敛于期望值

难点：如何让计算机生成满足p(x)的样本

解决方案：用p(x)的累积分布函数cdf(x)的逆函数来生成服从p(x)的样本

难点：累积分布函数cdf(x)的逆函数在p(x)复杂时难以计算

解决方案：见下

2.拒绝采样=接受-拒绝采样

p(x)难以采样 => 引入容易的采样的分布q(x) 称为提议分布 => 以某**标准**拒绝一部分样本 => 最终采集的样本浮层p(x) 【kq(x)覆盖未归一化的分布p(x)——kq(x)≥p(x)】

标准：每次抽取样本的接受概率

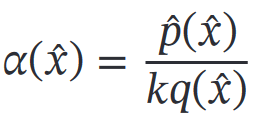
判断拒绝采样的好坏：拒绝率太高，采样效率会不理想

3.重要性采样

思想：我只是想算那个期望（𝔼𝑝[𝑓(𝑥)]），抽取的样本其实不用严格服从p(x)，所以用提议分布q(x)直接采样并估计期望

w(x)是重要性权重

4.马尔可夫链蒙特卡罗方法 MCMC

思想：将采样过程看成马尔可夫链——第t+1次采样依赖于第t次抽取的样本和状态转移分布（即提议分布）

关键：构造出平稳分布为p(x)的马尔可夫链，且状态转移分布容易采样

预烧期：马尔可夫链需要一段时间的随机游走才能达到平稳状态，这个时期内的采样点要丢掉！

（1）Metropolis-Hastings算法=MH算法

动机：状态转移分布（提议分布）的平稳分布往往不是p(x)

思想：引入拒绝采样来修正提议分布，使最终采样的分布为p(x)

与拒绝采样的区别：第t+1次采样样本的接受概率和第t次所采样的样本有关系！

（2）Metropolis算法

在MH算法基础上，加限定条件：提议分布是对称的

这样使得接受率公式简化了！

（3）吉布斯采样

可看作MH算法的特例

思想：使用全条件概率作为提议分布，对每个维度采样，设置接受率A=1

全条件概率：

每单步采样构成马尔可夫链。

5.几种方法的对比

拒绝采样、重要性采样——效率随空间维数的增加而指数降低

马尔可夫链蒙特卡罗方法——容易对高维变量进行采样

第12章 深度信念网络

一、玻尔兹曼机

1.形式

看图理解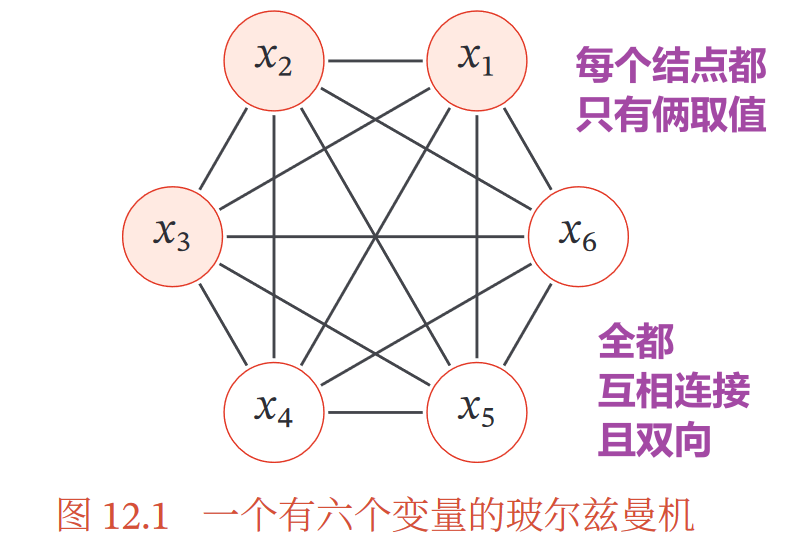

2.玻尔兹曼分布


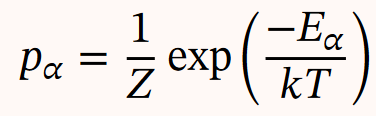𝐸_𝛼 为状态 𝛼 的能量，𝑘 为玻尔兹曼常量，𝑇 为系统温度, exp( −𝐸_𝛼 /𝑘𝑇 ) 称 为玻尔兹曼因子

3.玻尔兹曼机

（1）概念


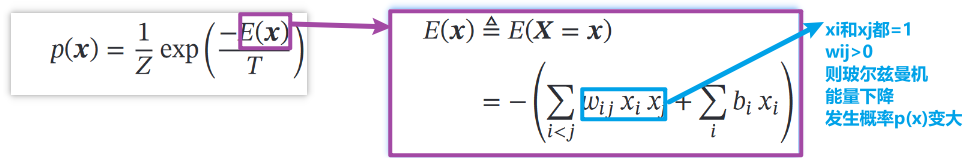x_i 取值1表示模型接受x_i代表的假设，取值0代表模型拒绝x_i代表的假设

w_ij表示两个假设间的弱约束关系，为正说明相互支持，可能被同时接受，为负反之

（2）应用

①解决搜索问题

②解决学习问题

4.生成模型——以基于吉布斯采样生成样本为例

过程：

①随机选择变量X_i

②根据全条件概率设置状态为1或0


③固定温度T下运行足够时间，达到热平衡

T → ∞ ： 可以很快达到热平衡

T → 0 ： 变成确定性方法，退化成Hopfield网络

④此时任何全局状态概率服从玻尔兹曼分布p(x)，只与系统能量有关，与初始状态无关

5.能量最小化与模拟退化

（1）能量最小化

简单、确定性方法如Hopfield网络，会收敛到局部最优解而不是全局最优

（2）模拟退火

目的：作为寻找全局最优的近似方法

过程：刚开始在高温运行达到热平衡，然后逐渐降低，直到低温也达到热平衡

6.参数学习

学习的参数是：W和b

定义对数似然函数后求偏导

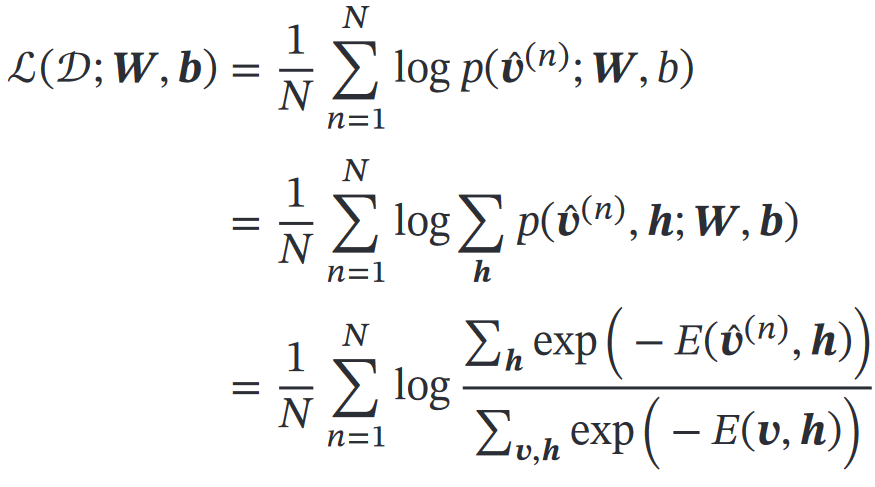
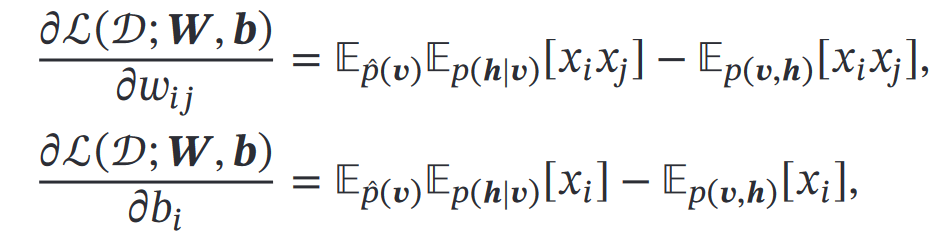
涉及计算配分函数和期望，难精确计算，所以用MCMC方法来近似求解：

固定住可观测变量 𝒗，只对 𝒉 进行吉布斯采样

=> 达到热平衡，采样x_i x_j的值

=> 近似期望

二、受限玻尔兹曼机

玻尔兹曼机每更新一次权重就要重新热平衡，低效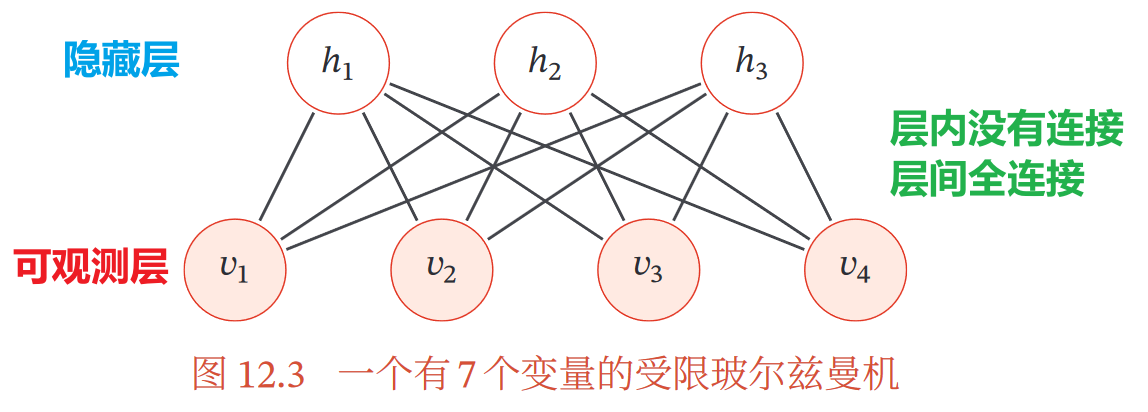

规定能量函数和联合概率分布：

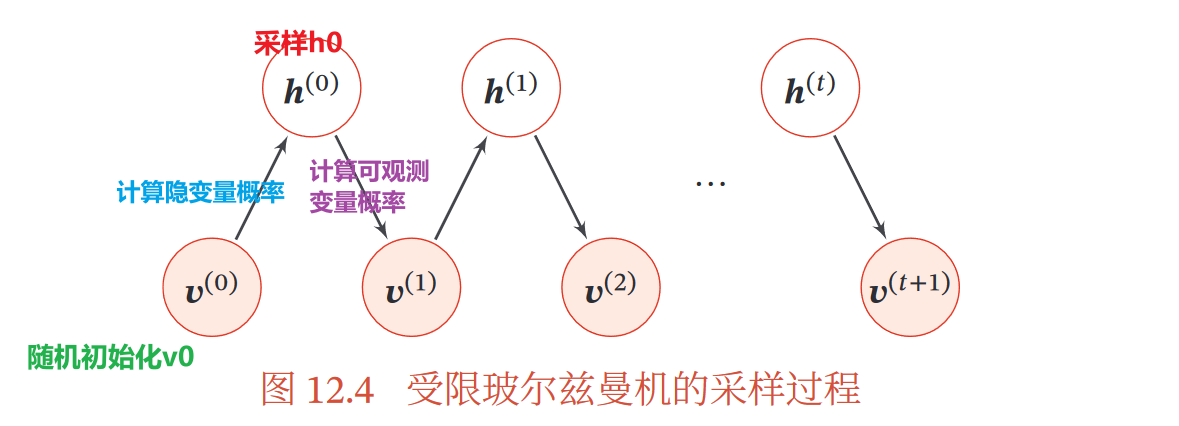
1.生成模型

给定联合分布概率：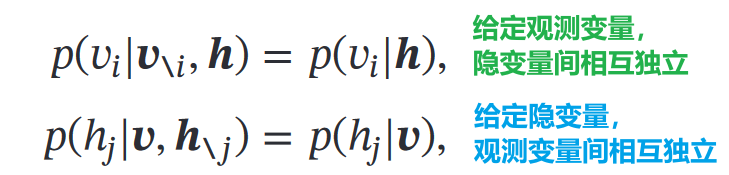

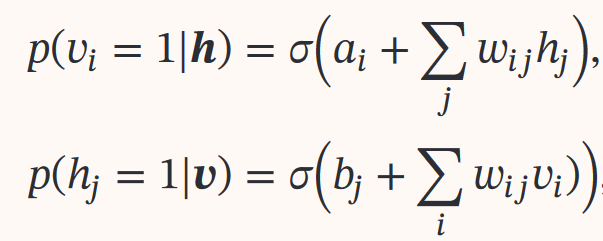
吉布斯采样：

2.参数学习

要学习的参数：W a b

方法：最大化对数似然函数

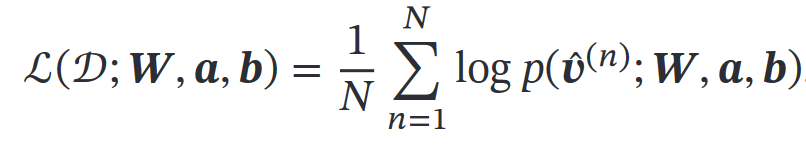
求偏导

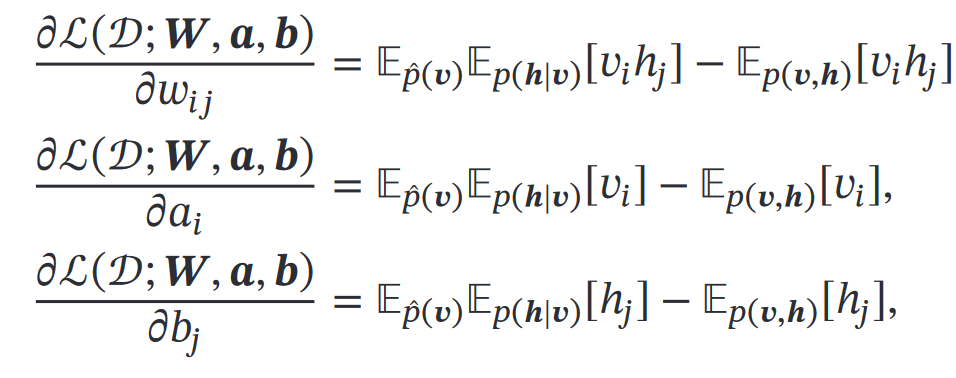
要算配分函数和俩期望，难算，用MCMC方法近似：

 固定v并设为训练样本中的值，根据条件概率对h采样，

 再不固定v，通过**吉布斯采样**轮流更新v和h，达到热平衡采集v和h的值

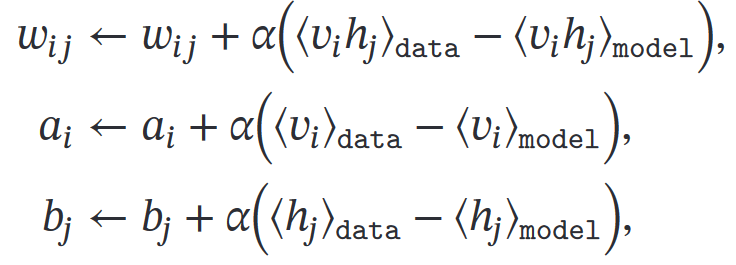
对比散度学习算法（对受限玻尔兹曼机来说，比吉布斯采样更有效）

【CD-k算法】

用一个训练样本作v的初始值 => 交替对v和h进行吉布斯采样 =>不需要等到收敛，k步足够

3.受限玻尔兹曼机的类型

（1）伯努利-伯努利 受限玻尔兹曼机

（2）高斯-伯努利 受限玻尔兹曼机

（3）伯努利-高斯 受限玻尔兹曼机

三、深度信念网络 DBN


有：

且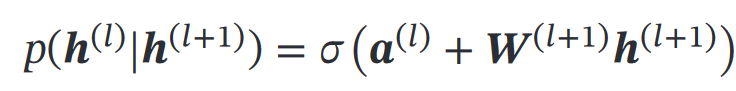

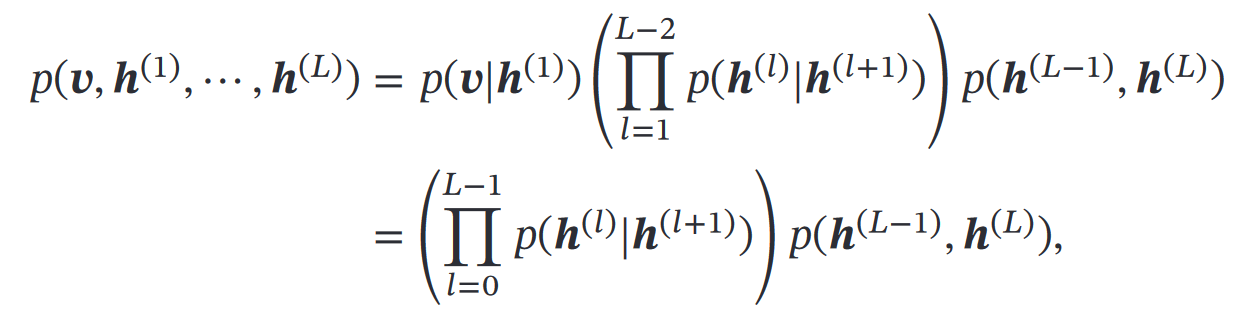
1.生成模型

生成样本过程：

运行顶层受限玻尔兹曼机，进行足够多次吉布斯采样

=>达到热平衡，生成样本h^(L-1)

=>计算下一层变量条件分布+采样

=>continue

2.参数学习

过程：

每层Sigmoid信念网络转化成受限玻尔兹曼机【隐变量后验概率相互独立】

=>逐层训练【自底向上，每次训练一层，训练包括俩阶段：逐层预训练、精调】

（1）逐层预训练


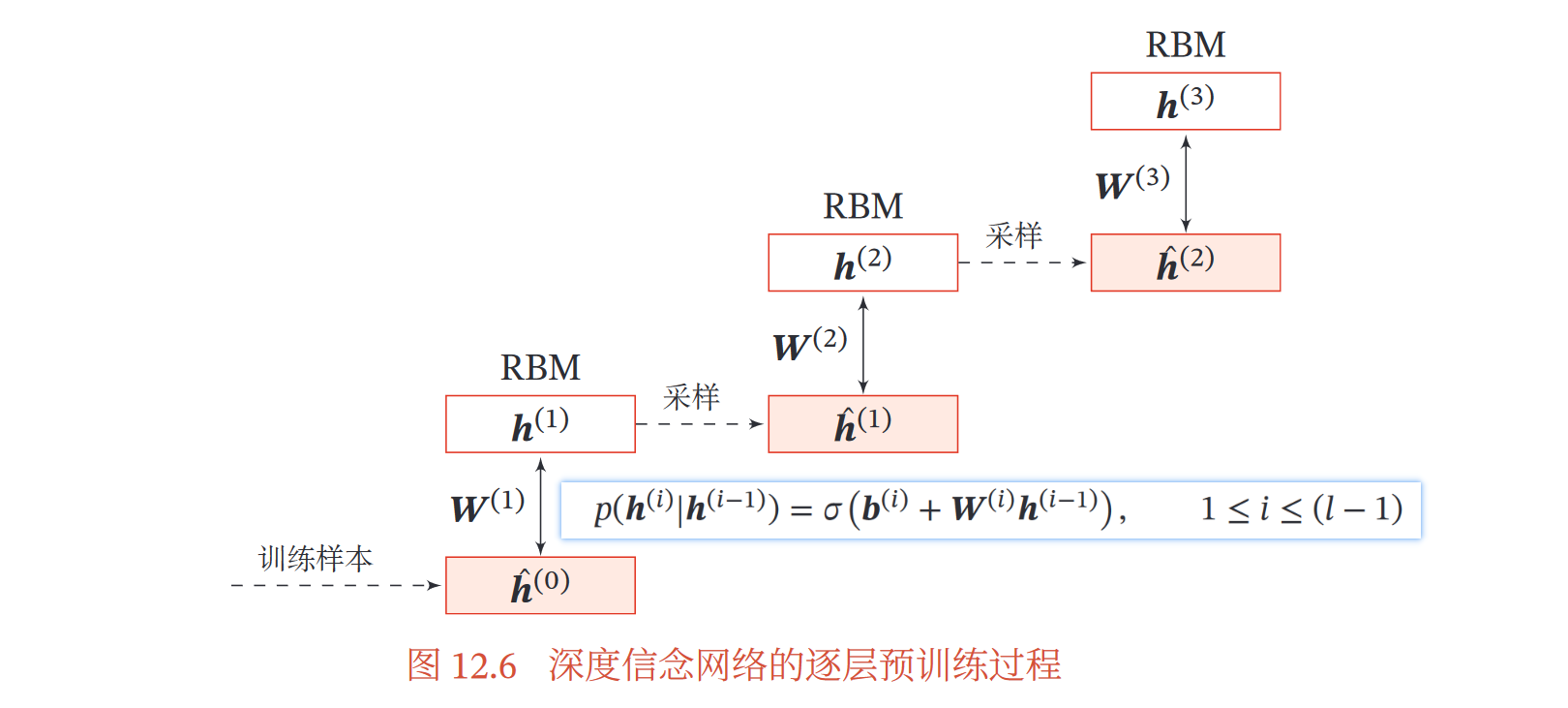
（2）精调

①作为生成模型的精调


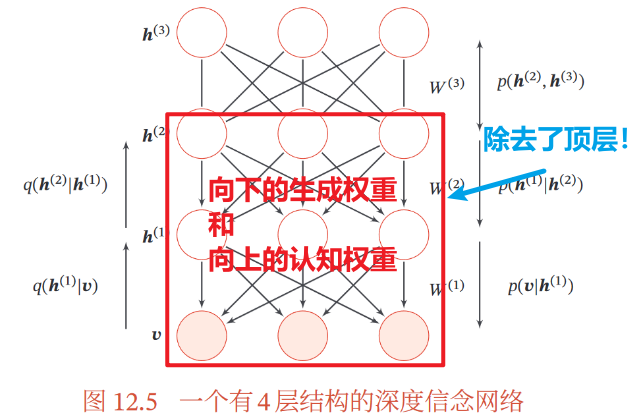生成权重：向下的 | 定义原始生成模型

认知权重：向上的 | 反向计算上行的条件概率

Wake-Sleep算法


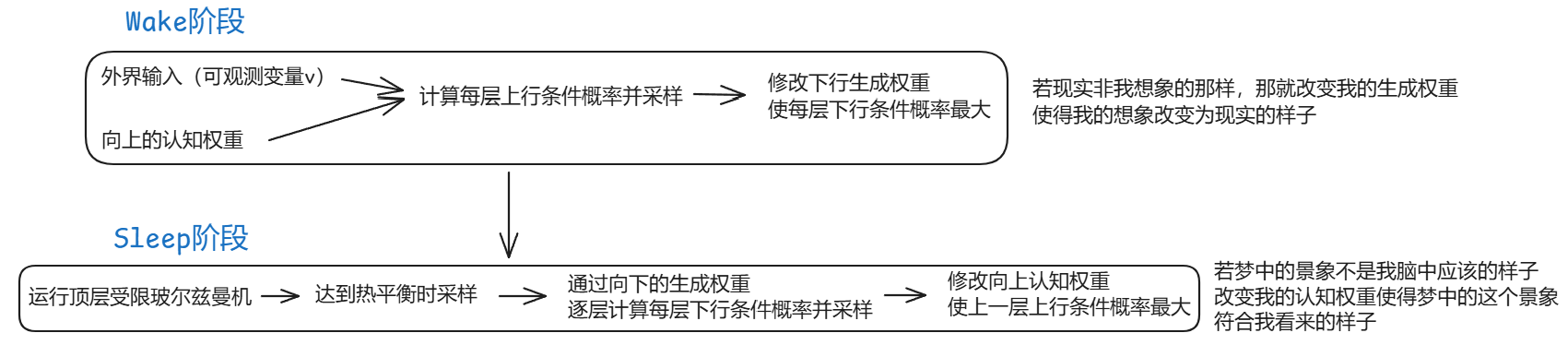交替两个阶段直到收敛

②作为判别模型的精调

在深度信念网络的最顶层再增加一层输出层，然后使用 反向传播算法 对这些权重进行调优

第13章 深度生成模型

概率生成模型=生成模型：

根据可观测样本，学习参数化模型，近似未知分布，生成与真实样本相近的样本

     <font style="color:#DF2A3F;">概率密度估计    </font>            <font style="color:#DF2A3F;">生成样本（采样）</font>

深度生成模型：

利用深度神经网络建模复杂分布/生成符合分布的样本

一、概率生成模型

1.密度估计

概念：根据数据集估计它的概率密度函数pde

难点：不存在复杂依赖关系，难用图模型

解决：引入隐变量，用EM算法

问题：EM算法需要估计的条件分布比较复杂的时候咋整？

解决：变分自编码器——用神经网络建模

2.生成样本=采样

概念：给定pde，生成相应样本

过程：在EM算法中，隐变量先验分布采样+条件分布采样

生成对抗网络的思想：从简单分布中采集出的样本，送到神经网络里，使得输出服从我们的分布，避免了密度估计

3.应用于监督学习

典型：朴素贝叶斯、隐马尔可夫

on opposite：判别模型 eg.Logistic回归、SVM、神经网络

关系：生成模型可得到判别模型，反之不成立

二、变分自编码器

为了得到，拆解为：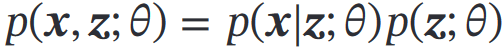

假设拆解后的这两个分布都服从某种参数化分布族，则用最大似然来估计

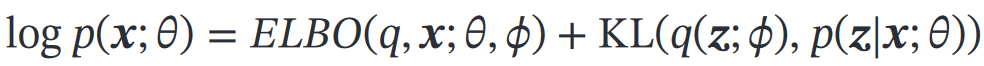
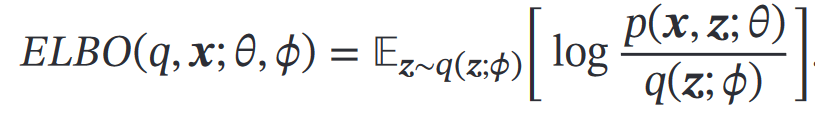
其中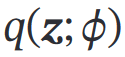是额外引入的变分密度函数

最大似然过程用EM：

E：寻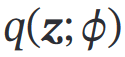等于/接近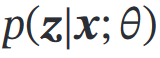

M：固定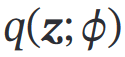，找θ，最大化ELBO

理论最优=：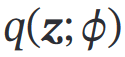

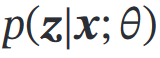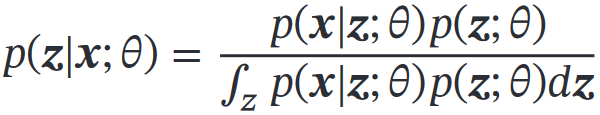，但这个不好计算

解决方案：变分推断，近似估计，用简单的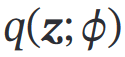来近似推断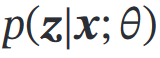

问题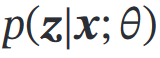：一般复杂，近似效果不好，也难用已知分布族函数建模

解决方案：变分自编码器

解决具体方式：

用神经网络估计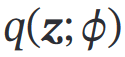（近似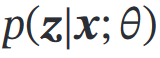）——这个神经网络称为推断网络——输入x，输出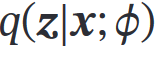

【推断网络的目标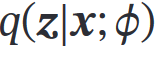：尽可能接近真实后验 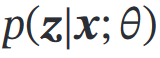=> 最小化KL => 找到网络参数**𝜙∗**使得ELBO最大】

   用神经网络估计![](https://cdn.nlark.com/yuque/0/2024/png/40781129/1734872812773-687a53bd-48f6-4afe-a15c-49425ffef82a.png)——这个神经网络称为生成网络——输入z，输出![](https://cdn.nlark.com/yuque/0/2024/png/40781129/1734872799769-2ccebd70-c4ed-43da-9454-6839272596b3.png)

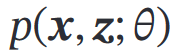（可分为 隐变量 𝒛 的先验分布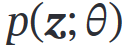和条件概率分布）

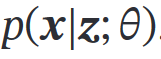【生成网络的目标：找到网络参数**θ∗**使得ELBO最大】

【注意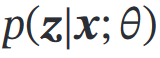和 和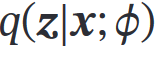not the same】

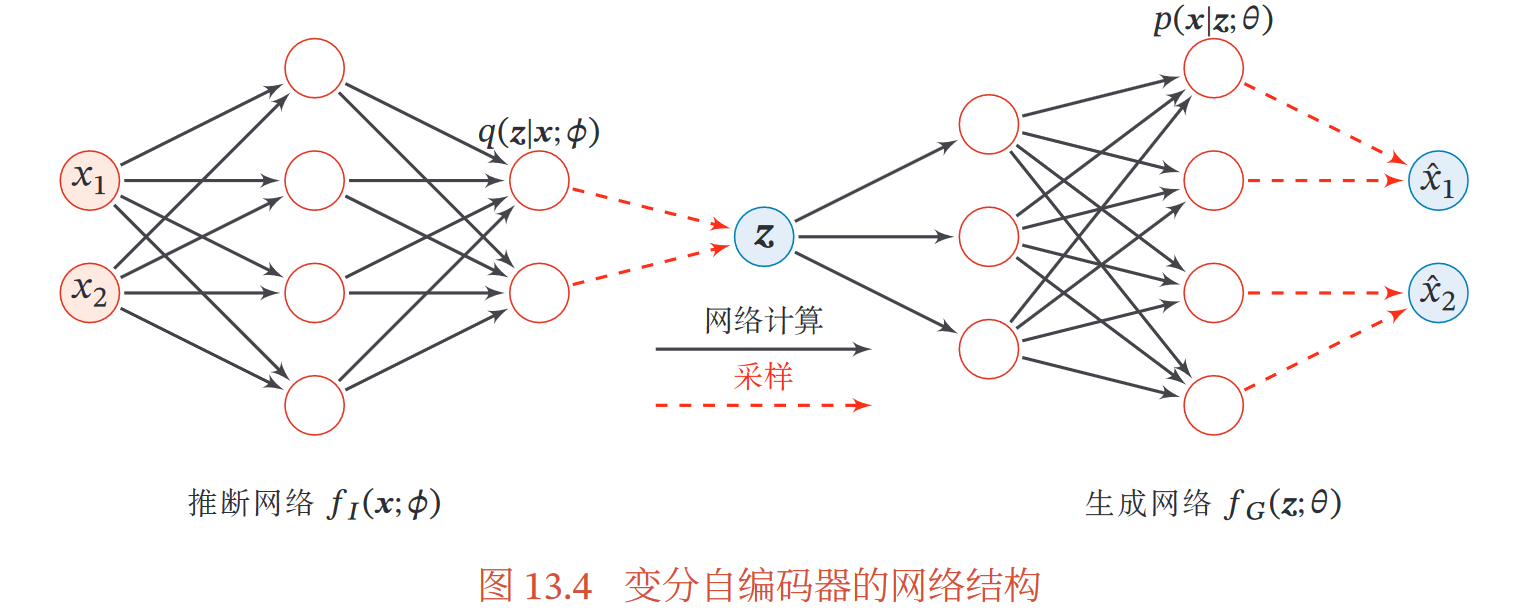
汇合推断网络和生成网络的目标（都是使证据下界ELBO最大）：

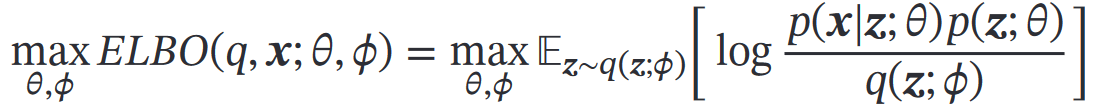
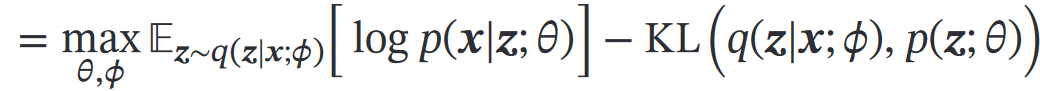
再参数化：𝑓(𝜃) 的参数 𝜃=𝑔(𝜗)，则 𝑓(𝜗)= 𝑓(𝑔(𝜗))

引入分布为𝑝(𝜖) 的随机变量 𝜖，把目标的第一项期望写成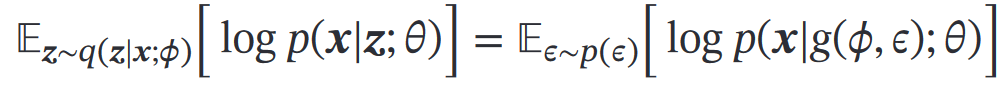

假设第二项的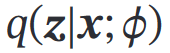有：

通过再参数化，可用梯度下降法来学习参数