计算机视觉知识点总结（结合cs131）

〇、考点

题目主要集中在分割之前

1. 绪论

• 知道几个计算机视觉的应用场景（选择题）

2. 图像的形成

• 颜色直方图的优缺点

3. 图像处理基础

• 卷积时对边缘填坑问题的四种处理方式，对应matlab函数的意义
• 高斯核方差/窗宽的变化与平滑程度的关系（可能简答可能选择）
• 常见卷积核（原图、左移一个单位、模糊…）
• 高斯核的自卷积性质
• 卷积时间复杂度分析（强调了一定会考）

4. 边缘检测

• 解释为什么图像对x（y）求导提取了y（x）方向的特征
• 可分离性的证明，可能是高斯核，也可能是高斯一阶偏导核（一定会考）
• 3.10没声，不知道Canny边缘检测器的考点情况
• 霍夫变换和RANSAC的异同点？（简答）
• 霍夫变换的流程的大致描述
• 霍夫变换的优缺点（可能选择也可能问答）

5. 拟合

• K-Means 算法的流程
• K-Means 算法的优缺点
• Mean Shift 算法的流程
• Mean Shift 算法的优缺点

6. 局部特征

（1）角点检测

• Harris角点检测的流程
• M矩阵和阈值R如何计算
• Harris角点检测的不变性

（2）斑点检测

• 高斯差分如何提升了计算效率
• 高斯核的性质（高斯核的自卷积性质）

（3）纹理特征

• 优点、属性（可能以选择题的形式）
• SIFT特征的维度（128）
• 需要好好复习SIFT特征

7. 分割

不知道

8. 识别

不知道

9. 检测

• Boosting算法的思想
• 统计模板方法的优缺点（选择题）

一、绪论

1. 计算机视觉的目标

跨越“语义鸿沟”建立像素到语义的映射

2. 人类视觉系统

（1）视觉流程

图像/视频 → 眼睛【感知设备】 → 大脑【解释器】 → 花草树木 春夏秋冬 山河湖海…【解释】

（2）能力

• 运动视盲
• 分割
• 感知
• …

（3）计算机视觉的应用场景

• 三维重建
• 人脸检测、笑容检测
• 虹膜识别、指纹识别
• 手写字体识别、车牌识别
• 无人超市
• 火星探测
• 医学图像辅助诊断
• 增强现实
• 虚拟现实
• …

这部分没什么东西，略过

二、图像的形成

1. 图像的类型

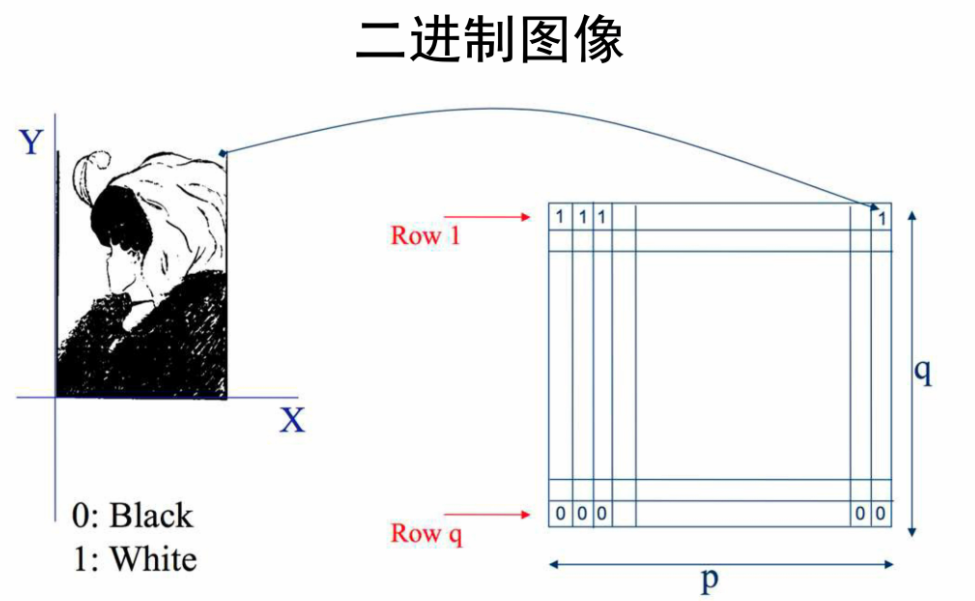
（1）二进制图像

每个像素点取值0/1；0黑，1白
每个像素点可以用1个bit表示

（2）灰色图像

每个像素点取值0~255；小黑，大白
每个像素点可以用1个byte表示（$1$ $byte$ = $2^8$ $bit$= $256$ $bit$）

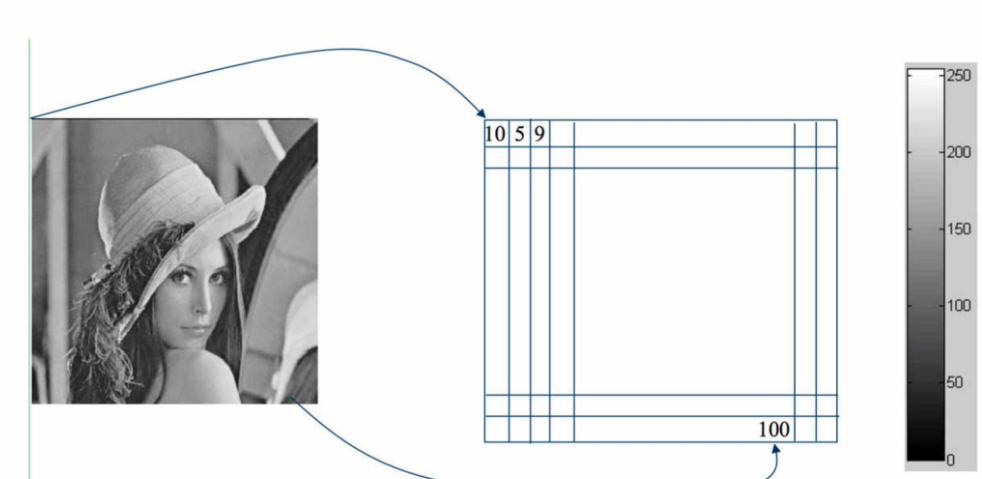
灰度图像能表示的信息有限，比如车道的黄线和白线，灰度表示不出来

（3）彩色图像

eg.RGB

三个通道：Red/Green/Blue
每个像素点可以用3个byte表示

2. 数字图像的存储

对数字图像进行采样和量化两个操作，从而表示为整数值矩阵

（1）采样

在一个规则的网格上对二维空间进行采样：

• 把图像划分为非常多的小格子，格子越多，分辨率越高，每个格子表示一个像素
  

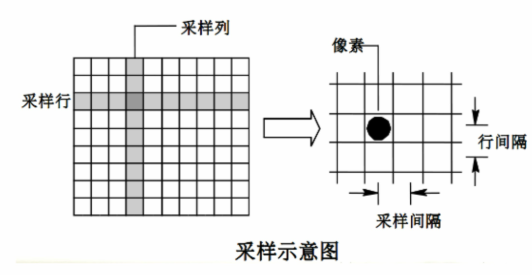
（2）量化

• 给每个小格子（像素）一个整数值，0~255，数值连续
  

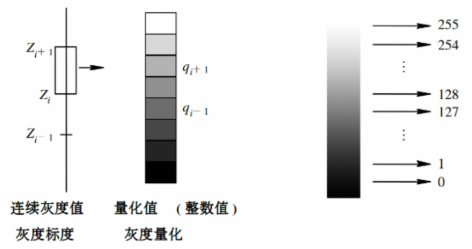
3. 图像色彩模型

（1）色彩空间的定义

通过多个颜色分量构成坐标系来表示各种颜色的模型系统

（2）常见的色彩空间

① RGB

Red/Green/Blue
红绿蓝，每个0~255，因此可以表示$256^3$种颜色

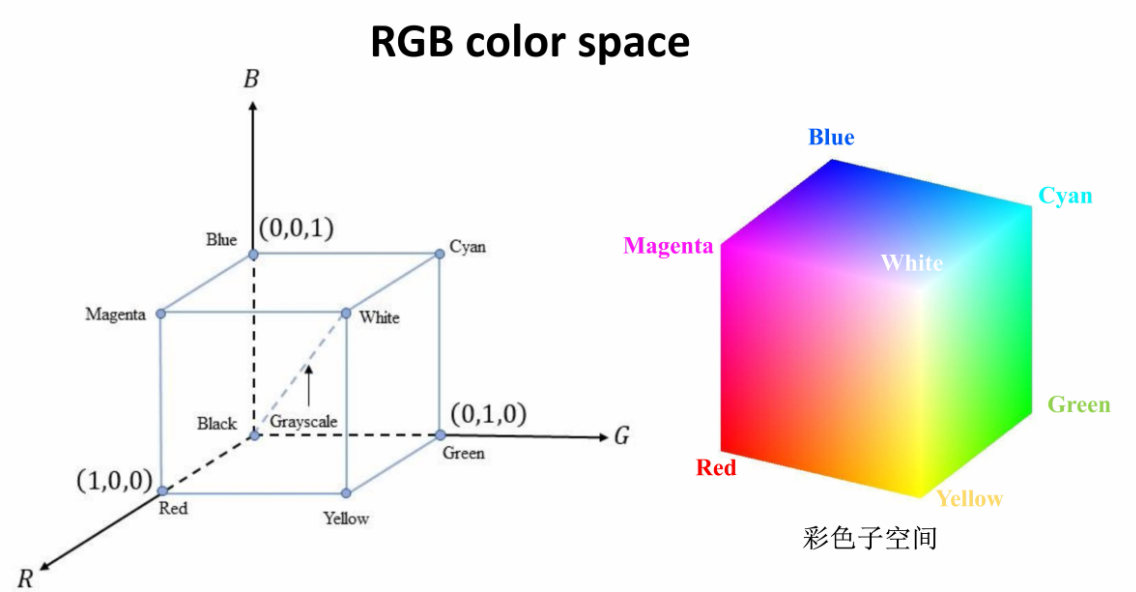
② HSV

Hue（色调）/Saturation（饱和度）/Value（亮度）

Hue的取值是0°~360°；Saturation的取值是0~1；Value的取值是0~1
HSV在图像增强领域应用的比较多，能够更大程度保护图像颜色信息，避免色彩失真

③ HLS

Hue（色调）/Lightness（亮度）/Saturation（饱和度）

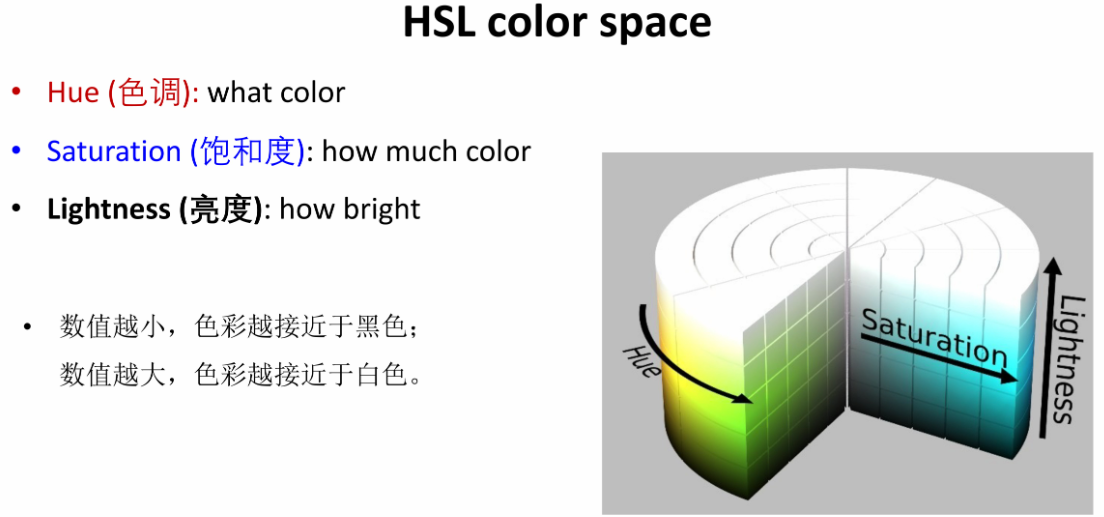
（图中说数值越大越小，色彩越白越黑，指的是）

Value和Lightness的区别

• Value：光线强度的明度
• Lightness：白色光线的多少

4. 图像直方图

（1）构建直方图示例（简单灰度图像示例）

直方图Histograms，初始化直方图有i个格子（bin）：H[i]
假设i=4，对如下图的图像构建直方图：

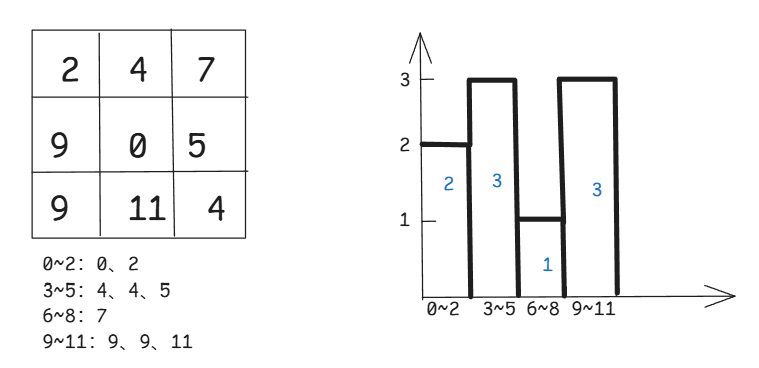
（2）归一化

① 动机

对于两个大小不同的图像，想要进行比较，如果都选取同样bin的数量构建直方图，则小的图像显然取值少，无法合理比较。

② 做法

按照原来的取值，除以总像素数量即可。
在刚才的例子中，相当于从 $2,3 ,1,3$ 变成 $\frac{2}{9},\frac{3}{9},\frac{1}{9},\frac{3}{9}$

（3）彩色图像构建直方图——颜色直方图

① 构建方法

a. 方法1：分别构建三个通道的直方图

b. 方法2：三个通道取均值/按比例得到一个数值，再构建一个直方图

② 颜色直方图的优点

• 颜色直方图可以比较好的表示一张图像
• 计算过程快速且计算方式简单
• 可以将大小进行标准化，从而比较不同的图像直方图
• 可以利用颜色直方图进行数据库查询或分类

（4）总结bin与像素的关系

• 每个像素都有且只有一个自己所属的bin
• 每个bin可能会对应多个像素

三、图像处理基础

1. 噪声的去除

如果能和周围的像素加权平均一下，噪声点的影响就变小了
因此可以把加权平均的权值做成一个卷积核/滤波核

2. 卷积

（1）卷积核

① 卷积核的意义

存储了当前点和周围点的加权平均的权值

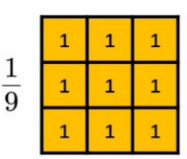
例如上图，$\frac{1}{9}$其实是需要乘到每个小方格里面的
那么以中间的$\frac{1}{9}$为例子，它就是由周围的$9$个$\frac{1}{9}$，加起来后除以$9$，进而得到的

② 卷积的定义

假设$f$是图像，$g$是卷积核：

$$(f * g)[m,n] = \sum_{k,l} f[m-k, n-l] g[k,l]$$

其中：
$m,n$是卷积模板最中间位置的坐标
$k,l$是翻转后卷积核的坐标，取值范围是$-1,0,1$
$g[k,l]$是翻转后的卷积核在(k,l)位置的值
我认为需要结合一个例子来解释更清晰：

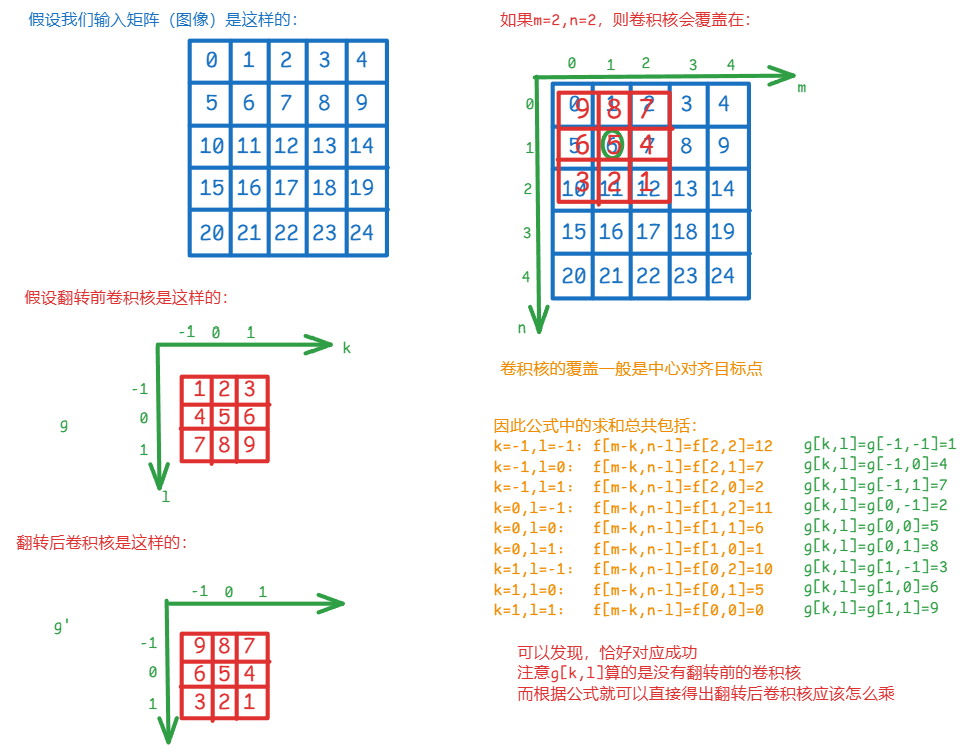
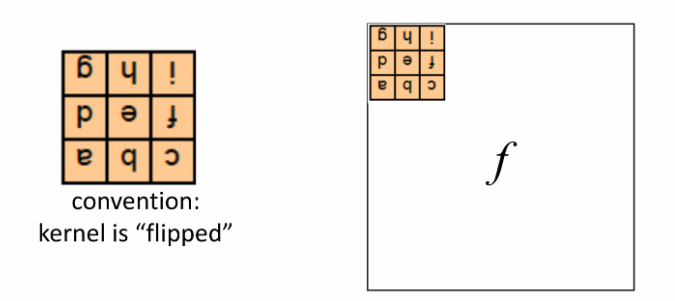
关于卷积核的翻转：
老师的PPT中翻转是垂直翻转，但实际上严格的卷积翻转是垂直+水平，也就是中心旋转180°
考试中如果提到翻转还是默认以老师PPT中的垂直翻转为准
上面的卷积公式，只有在中心旋转时才生效！否则不生效，是错误的！

③ 卷积的理解

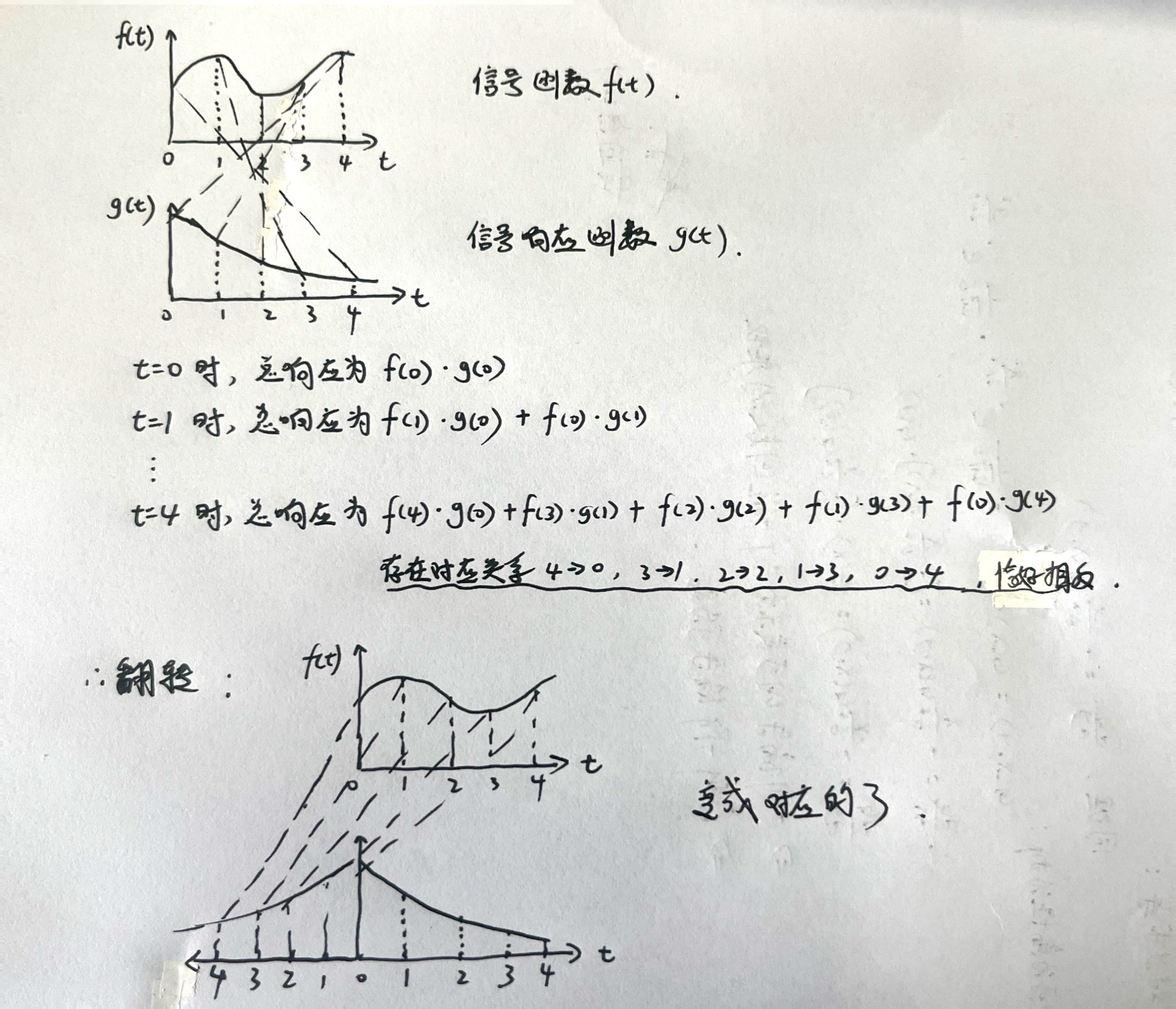
因此卷积做了翻转：

（2）卷积操作的特性

① 线性

$$filter(f_1+f_2)=filter(f_1)+filter(f_2)$$

即$f_1,f_2$两张图像先求和在做卷积，等于分别卷积后在求和

② 平移不变性

$$filter(shift(f))=shift(filter(f))$$

即一张图像先做平移还是先做卷积，结果是一样的
推论：任何剪平移不变的操作，都可以用卷积来表示

③ 一些数学特性

• 交换律：$a*b=b*a$
• 结合律：$a*(b*c)=(a*b)*c$
• 分配律：$a*(b+c)=(a*b)+(a*c)$
• 数乘结合律：$ka*b=a*kb=k(a*b)$
• 对于单位脉冲信号$e=[...,0,0,1,0,0,...]$，有$a*e=a$

（3）卷积核覆盖与图像大小的关系

matlab函数中通过指定shape，存在三种覆盖模式

• full：卷积后图像会变大一圈
• same：卷积后图像会保留原始尺寸
• valid：卷积后图像会变小一圈

（4）卷积边缘填坑问腿

对于上面的same模式，由于卷积核部分在目标区域外，落在周围那一圈是我们需要填充的，有下面几个填充方法：

① Clip filter（black）

就是常数填充
填充一圈黑的，会出现黑边，不太好
对应matlab：imfilter(f,g,0)

② wrap around

填充的那一圈是从图像中随机采样的
对应matlab：imfilter(f,g,‘circular’)

③ copy edge

填充的那一圈是把边缘继续延伸进去的
对应matlab：imfilter(f,g,‘replicate’)

④ reflect across edge

填充的那一圈是沿着边缘镜像过去的
对应matlab：imfilter(f,g,‘symme’)

（5）常见卷积核

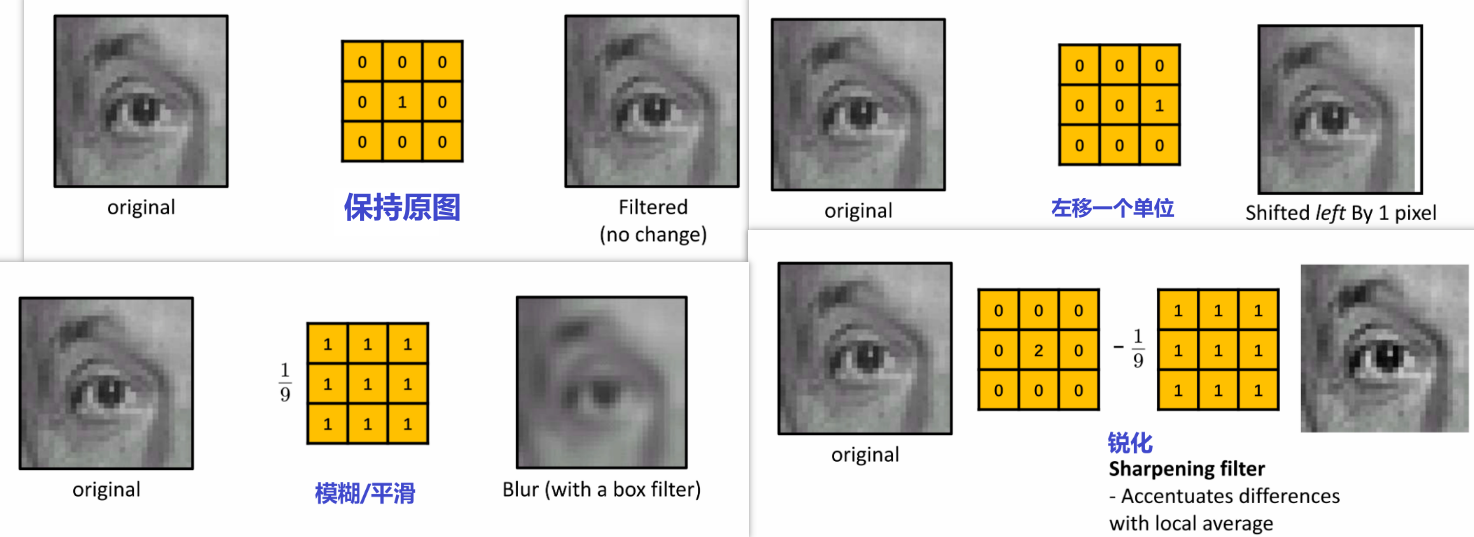
锐化的原理：
模糊/平滑卷积核相当于提取了平滑的特征，原图减去这些平滑的就剩不平滑的部分了，再加回原图相当于加强了。因此一共存在两倍的原图，所以在上面存在一个2

$$f*(2e-g)$$

同时，可以设置一个$α$在第二步加回去的突出部分前面，从而控制加回去多少细节，进而控制锐化强度，则有：

$$f + \alpha (f - f \ast g) = (1 + \alpha)f - \alpha f \ast g = f \ast ((1 + \alpha)e - \alpha g)$$

（6）卷积核的有效性

① 动机

• 卷积核通过与图像的像素值进行加权求和，提取特定的特征（如边缘、纹理）或实现滤波效果（如模糊、锐化）。卷积核中每个值的大小决定了对应位置像素的权重，因此可以说卷积核的设计直接影响了每个像素对输出结果的“贡献”。
• 想要得到更加有效的卷积模板，则应该考虑图像每个像素的贡献来设计卷积核的每个值，贡献大设计值大，贡献小设计值小。
• 因此很容易想到大部分情况下，中心像素对任务贡献最大。因此希望设计卷积核中间值大，越往两边越小。

② 高斯核/高斯滤波

$$G_\sigma = \frac{1}{2\pi\sigma^2} e^{-\frac{(x^2 + y^2)}{2\sigma^2}}$$

高斯函数就是中间大两头小，非常符合上面我们的想法。

a. 参数$\sigma$（方差）

固定窗宽看方差变化的影响：

• $\sigma$越大，数据越分散，中心点峰值越小，卷积核中心值越小
• $\sigma$越小，数据越集中，中心点峰值越大，卷积核中心值越大
  
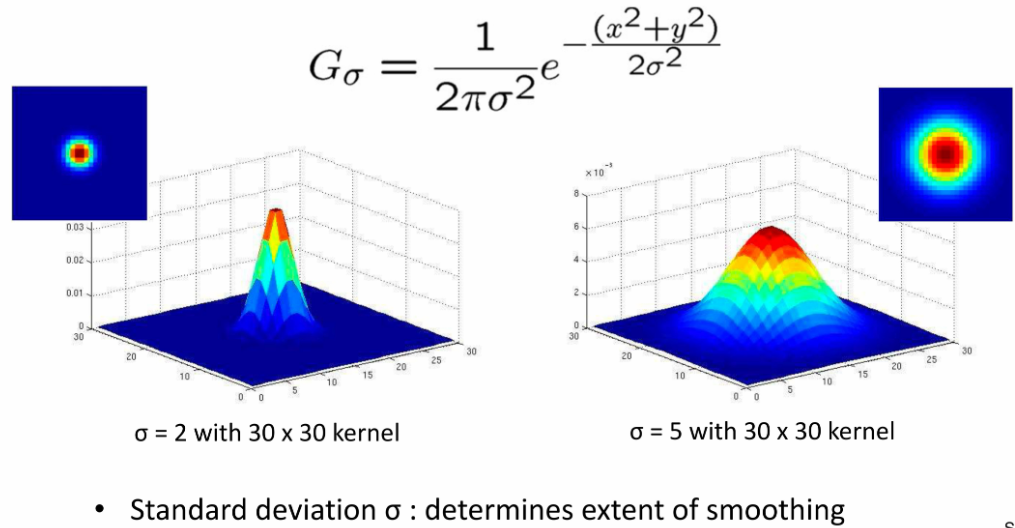
  因此$\sigma$可以控制平滑程度，形象点说，中心值越大说明对自己有很大的掌控权啊，平滑对我自己的影响就小，中心值小说明我容易丧失自我，就被平滑的很厉害~

b. 窗宽

固定方差看窗宽变化的影响：

• 窗宽越小，在归一化时分母越小，每个的权重就越大，平滑程度越大
• 窗宽越大，在归一化时分母越大，每个的权重就越小，平滑程度越小
  

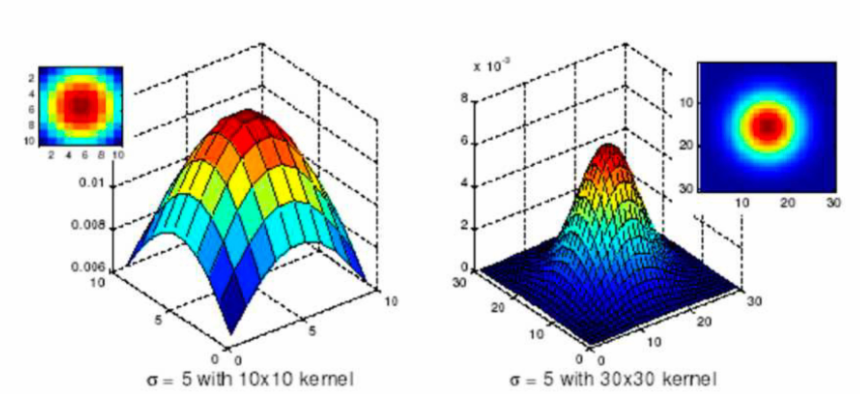
c. 现实中如何设置

根据经验值，窗宽的一半=三倍的方差
一般在现成的工具包中，指定一个方差，窗宽会自动给出

d. 高斯核的特性

• 作为低通滤波器，从图像中移除高频信号
• 高斯核的自卷积是另一个高斯函数，因此可以用小粒度高斯核的多次卷积，得到使用大粒度高斯核卷积相同的结果。 【重要！】
  
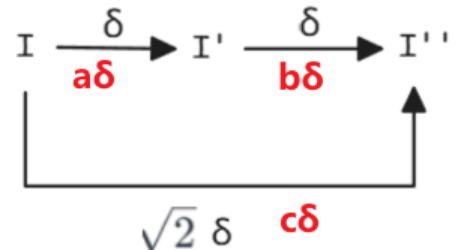
  图中的 $I$ 表示图像；同时这里符合勾股定理，$a^2+b^2=c^2$
• 一个二维的高斯函数可以拆分成两个一维的——可分离的函数
  可分离性的应用：
  
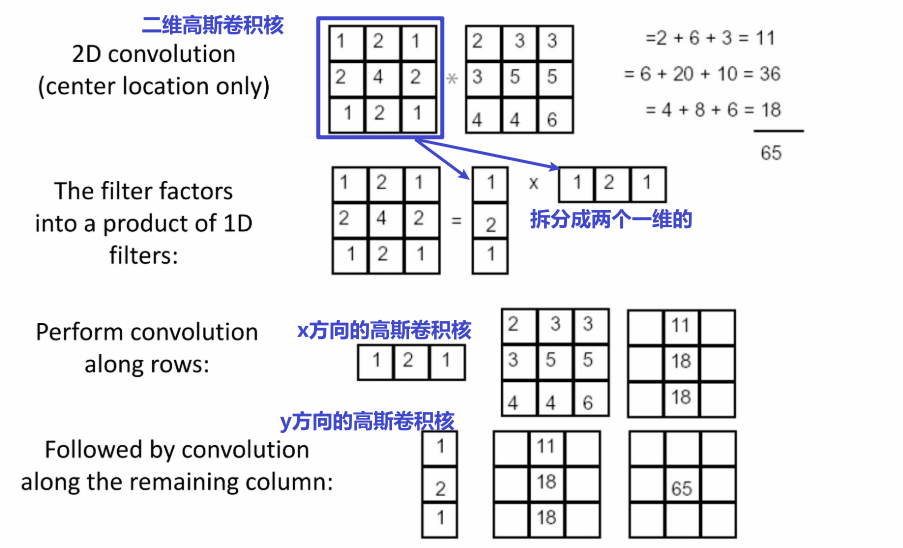
  就是一个拆分后逐步计算

（7）卷积的时间复杂度

$m×m$ 的卷积核 和 $n×n$ 的图像做卷积

① 一般情况

$O(n^2m^2)$

② 卷积核可分离的情况

$O(n^2m)$

3. 噪声

（1）噪声的种类

① 椒盐噪声（Salt and pepper noise）

像随机在图像上撒了一把“椒盐”，有黑的有白的

随机出现黑白像素

② 白噪声（Impulse noise）

随机出现白色像素

③ 高斯噪声（Gaussian noise）

出现从高斯正态分布得到的强度变化（叠加变量）

$$f(x, y) = \hat{f}(x, y) + \eta(x, y)$$

其中：

• $f(x, y)$ 是高斯噪声产生后的图像
• $\hat{f}(x, y)$ 是理想状态没有高斯噪声的清晰图像
• $\eta(x, y)$ 是高斯噪声，满足$\eta(x, y)$~$N(μ,σ)$ ，即服从高斯分布

（2）使用高斯滤波器去除高斯噪声

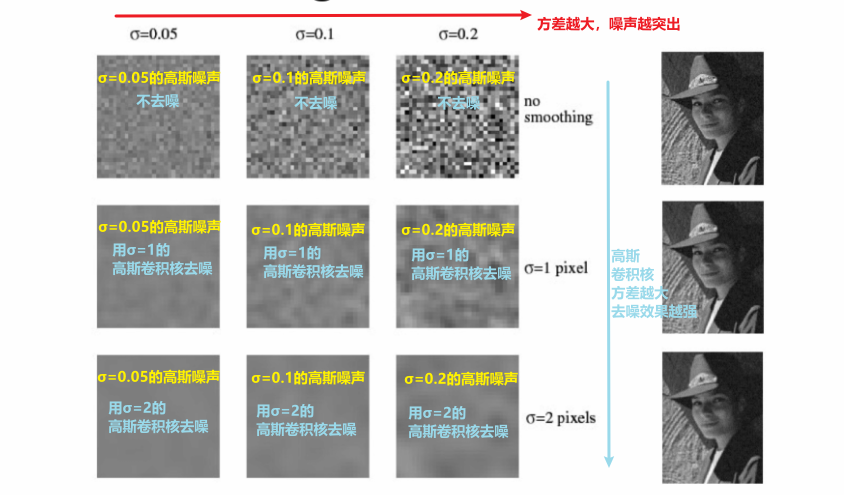
但上图也可以发现，大方差高斯卷积核虽然更能去除噪声，但也损失图像细节

（3）去除椒盐噪声

① 高斯卷积核效果不佳

用高斯卷积核去除椒盐噪声效果不理想：

大模板不仅没能更有效去除噪声，反而还损失了不少图像细节

② 中值滤波的步骤

a. 第一步：生成模板（3×3为例）

单纯一个3×3的框，里面啥也没有

b. 第二步：放到图像中取出像素值

c. 第三步：对其中的值找到中位数

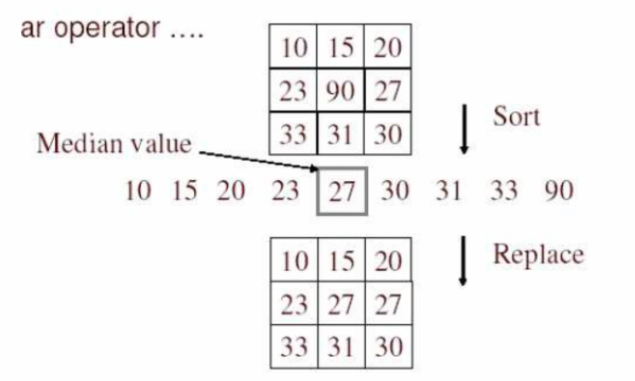
d. 第四步：用中位数替代模板最中间的值

Q：中值滤波是一个线性操作嘛？
A：不是，因为其中核心原理在排序，排序不是线性操作。

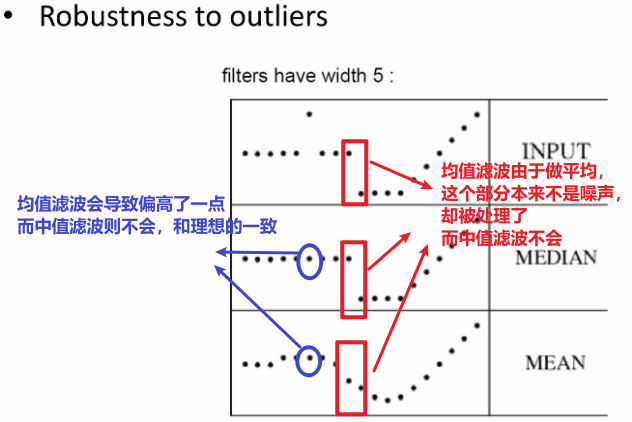
③ 中值滤波的优点

a. 擅长处理椒盐噪声、白噪声

b. 和均值滤波相比

四、边缘检测

1. 边缘基本概念

（1）边缘的定义

图像中亮度值明显而急剧变化的点

（2）研究边缘的意义

• 图像中大多数语义和形状信息可在边缘进行编码
• 相对于像素表示边缘表示更加紧凑
  图像→边缘→语义

（3）边缘的分类

• 表面法向不连续
• 深度不连续
• 表面颜色不连续
• 光照不连续
  

2. 边缘的提取

（1）思路

水平方向观察到像素值变化，强度函数求导找到极值点,极值点展示出边缘

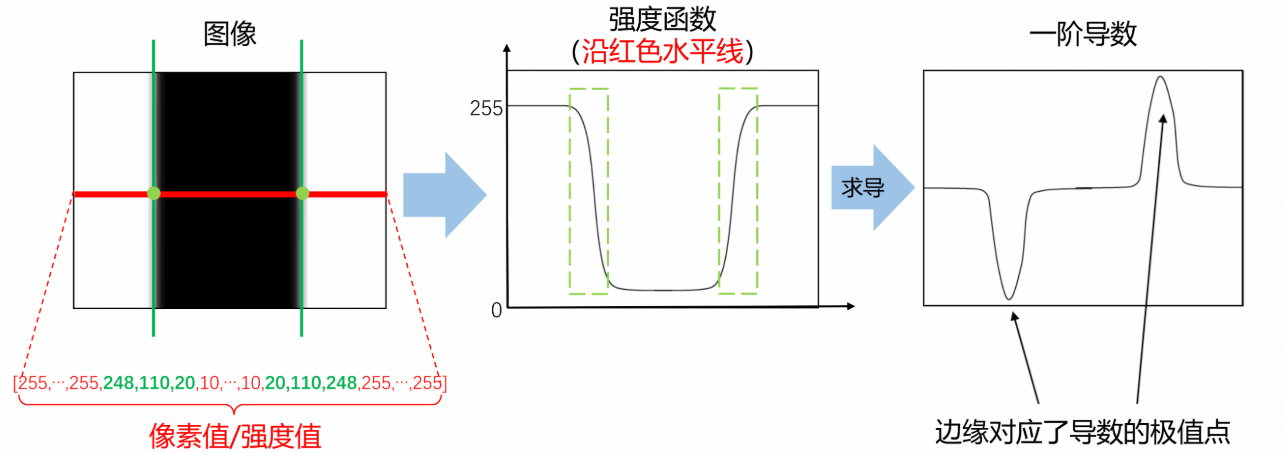
（2）图像求导

① 2D函数求导公式

$$\frac{\partial f(x, y)}{\partial x} = \lim_{\varepsilon \to 0} \frac{f(x + \varepsilon, y) - f(x, y)}{\varepsilon}$$

② 图像求导公式

图像是一个一个像素，是离散存储的，并不是上面那样连续的，因此只能取$\epsilon=1$来近似：

$$\frac{\partial f(x, y)}{\partial x} \approx \frac{f(x + 1, y) - f(x, y)}{1}$$

相当于右边的像素减去自己，就是导数了

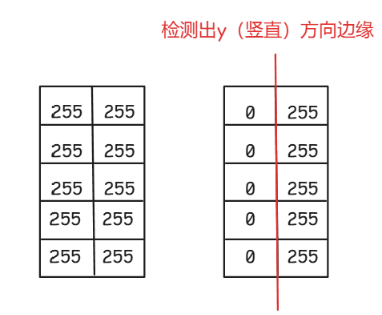
③ 用卷积实现图像求导

如图设计卷积核：

正好水平x求导就是右减左，竖直y求导就是下减上

④ 解释对不同方向求导得出垂直方向特征图像的原因【导数模板方向和信号方向是垂直关系】

解释：
对于x方向，求导相当于水平两个像素做差。

• 如果水平的两个像素差异不大，相减就相当于0，什么都没有了，导数为接近0，而前面说了，求导数后导数的极值点展示了边缘，所以没有展示出x方向的边缘。
• 如果水平的两个像素差异明显，同理，那么导数就得到了极值点，检测出y方向边缘。
  

⑤ 其他常见的导数滤波器（可略）

a. 简介

• Prewitt：利用像素点上下、左右邻点的灰度差。这种判定是欠合理的，会造成边缘点的误判，因为许多噪声点的灰度值也很大，而且对于幅值较小的边缘点，其边缘反而丢失了。
• Sobel：Sobel 算子在 Prewitt 算子的基础上增加了权重的概念，认为相邻点的距离远近对当前像素点的影响是不同的，距离越近的像素点对应当前像素的影响越大，从而实现图像锐化并突出边缘轮廓。
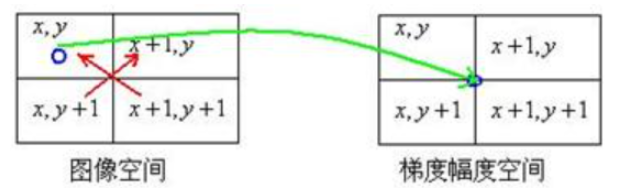
• Roberts：交叉算子边缘检测方法。该方法最大优点是计算量小，速度快。但该方法由于是采用偶数模板，如下图所示，所求的(x,y)点处梯度幅度值，其实是图中交叉点处的值，从而导致在图像(x,y)点所求的梯度幅度值偏移了半个像素
  

b. 总结

• Robert算子对陡峭的低噪声图像效果较好，尤其是边缘正负45度较多的图像，但定位准确率较差；
• Prewitt算子对灰度渐变的图像边缘提取效果较好，而没有考虑相邻点的距离远近对当前像素点的影响；
• Sobel算子考虑了综合因素，对噪声较多的图像处理效果更好。
  

（3）图像梯度

3. 噪声对边缘的影响

（1）影响

存在影响：

（2）原因

由于噪声的存在，找不到极值点了

（3）解决

① 流程

先去噪，再对信号求导，找到极值点

② 弊端

存在两次卷积，一次是去噪时卷积（$f*g$），另一次是求偏导时用导数模板做卷积求出偏导数，即上图红框的部分的求导过程。
当图像数量多的时候，由于存在两次卷积，计算量大

③ 弊端的进一步解决

利用卷积的结合性：$\frac{d}{dx}(f * g) = f * \frac{d}{dx}g$
也就是：

• 先对高斯核进行求导——得到 高斯一阶偏导核
• 再利用求导后的高斯核来和原始的有噪声的图像做卷积
  

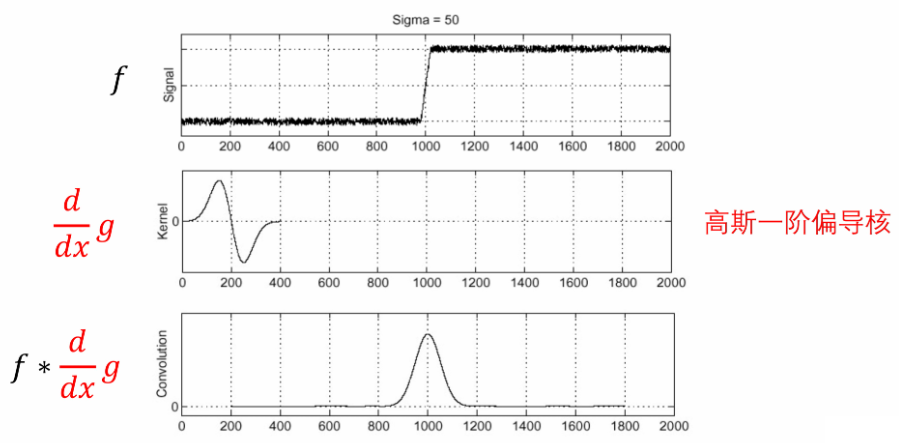
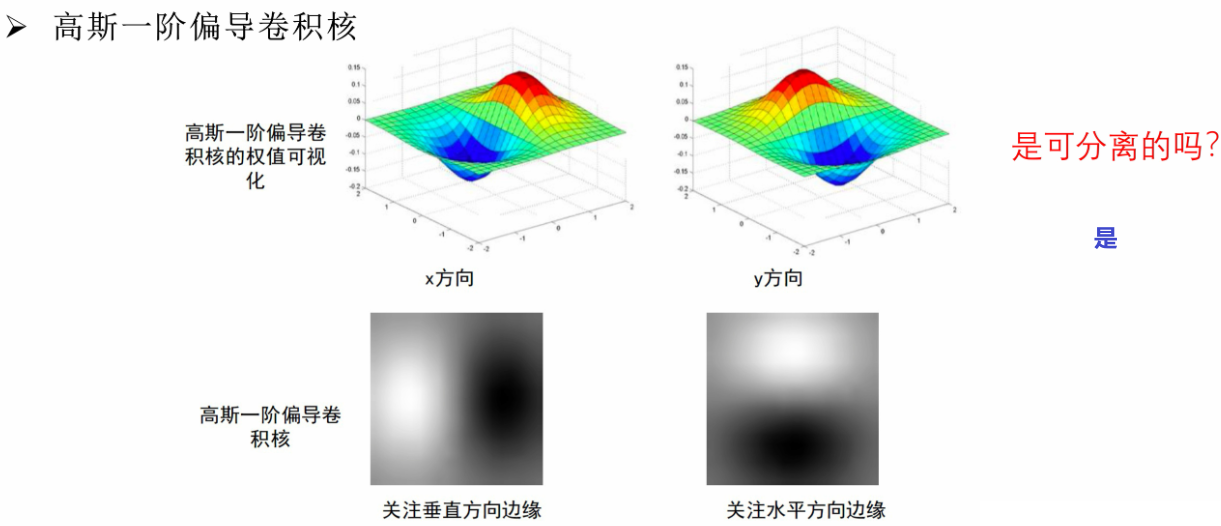
④ 高斯一阶偏导核

a. 可视化

看一下就行：

b. 方差的影响

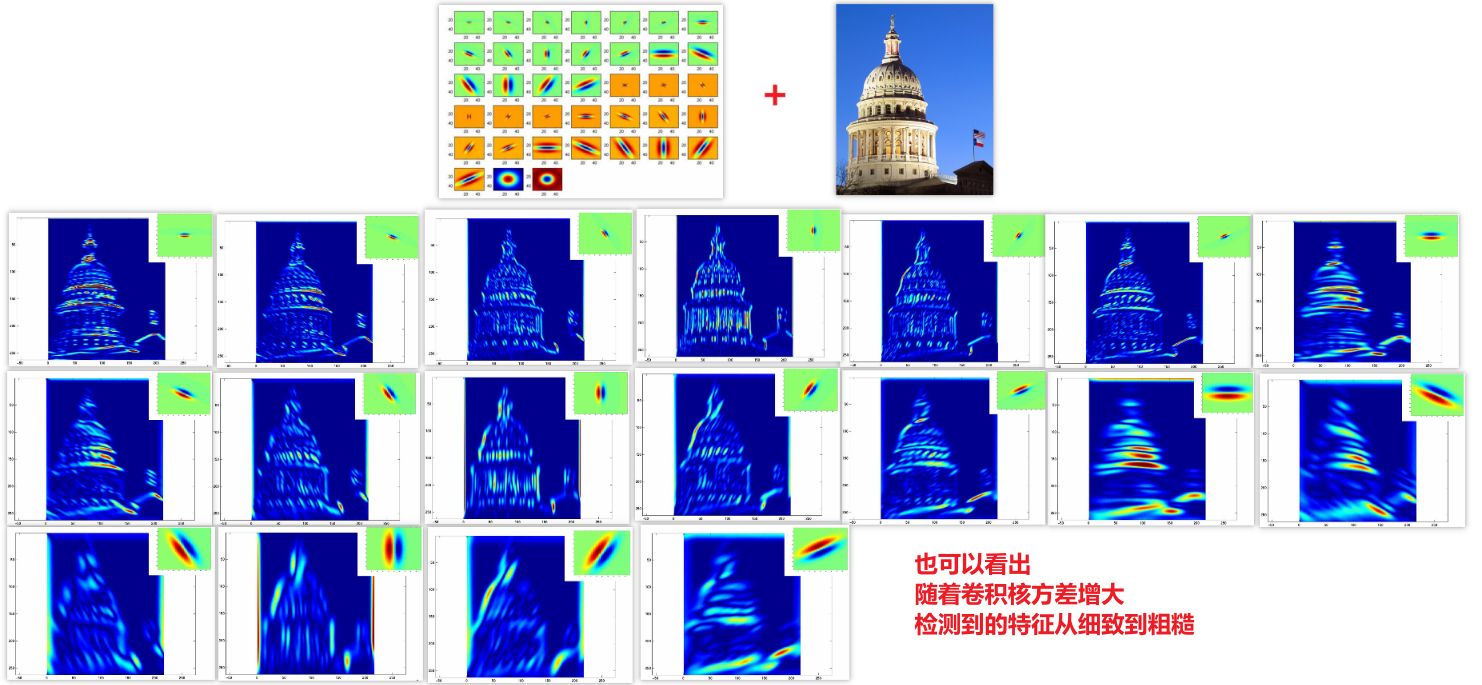
随高斯一阶偏导核方差变大，图像细节的丢失也会越来越严重

实际应用中，如果要识别细微的边缘特征，肯定方差设置小一点会好些；但如果只是想粗糙识别一下，比如看远方的一个物体是不是人，那方差设置大一点会好些，保留了轮廓信息
【就是看我们需要的轮廓是粗糙的还是细微的】

c. 可分离性证明

d. 高斯核 vs 高斯一阶偏导核

总结对比一下：

4. Canny边缘检测器

这部分智慧课堂无声，本人参考CS131专题-3：图像梯度、边缘检测（sobel、canny等）进行学习，感谢这篇博客。这篇博客恰好对应本章所有内容，相较课内更为详细，推荐学习。

（1）提出动机

常规边缘检测算法存在以下问题：

• 边缘很粗：如sobel这样的边缘检测算子，对图像求梯度图后，会设置一个阈值，绝对值超过阈值的像素为视为边缘，这就导致得到的边缘图中“边缘”会很粗
  
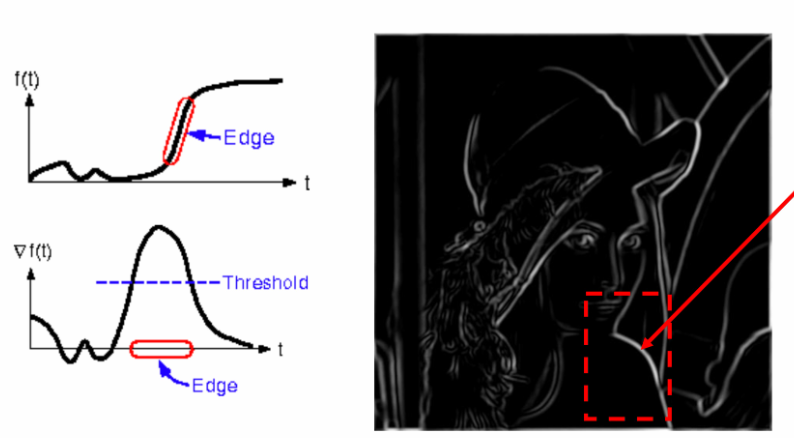
• 渐变边低于阈值，无法被识别为边缘：由于sobel中梯度阈值是全局性的，不能太高也不能太低，这就导致很多不明显的渐变边被擦除。
  

（2）Canny边缘检测器算法流程

matlab：edge(image,‘canny’)

① 对原始图像进行灰度化

此步课内PPT未提及，但是要进行的。因为边缘检测本质检测的是亮度变化。

② 对图像进行平滑（高斯滤波）

用高斯导数对图像进行滤波：对图像的x方向和y方向求梯度

③ 求图像平滑后的梯度图、以及梯度方向图

计算梯度强度（衡量是否为边缘）和梯度方向（用于非极大值抑制）

④ NMS非极大值抑制筛选

顾名思义就是在附近的一堆值中找到最大的那个，然后把不是最大的都设0

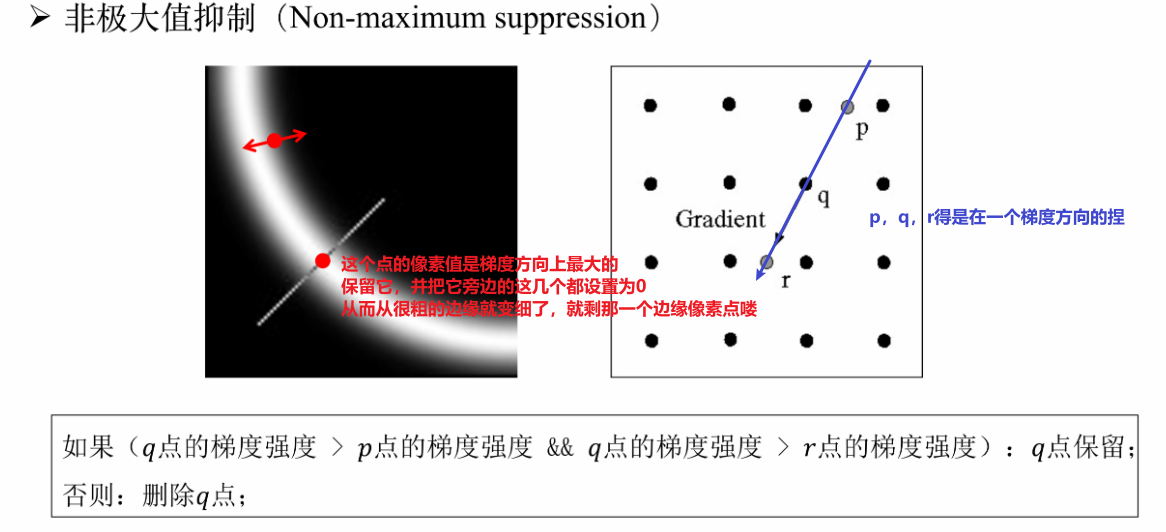
对比一下非极大值抑制的效果，明显变细了：

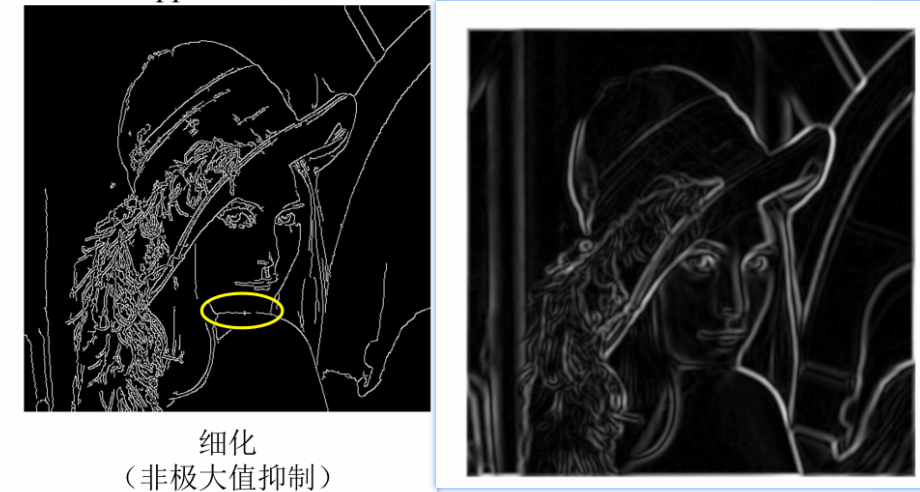
⑤ 双阈值+连通与否筛选

双门限法：定义两个阈值

• 高阈值：检测强边缘
• 低阈值：连接强边缘
  
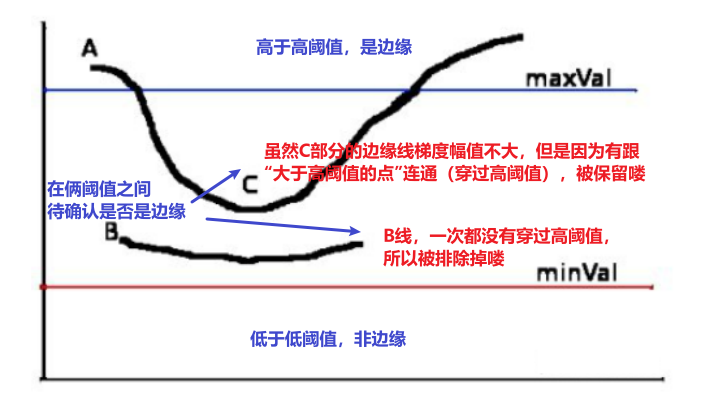
  简单来说就是高于高的就是边缘，低于低的就不是边缘，在中间的看有没有穿过高阈值的部分

补充

• 在②③两部分，实际中会采取之前说的先得到高斯一阶偏导核，再做卷积~
• 高斯核的方差$\sigma$越大，对图像平滑效果越强，越容易把边缘平滑掉，边缘会稀疏（仅保留非常明显的边缘）；反之，边缘会密集、详细。因此可控制方差大小获得想要的边缘图。
• Canny边缘检测的一些缺点：边缘可能不连续、边缘位置可能出现空间偏移（偏离真实边界）、方差的变化会明显改变结果，鲁棒性差。
  

5. 其他边缘检测技术（缺）

因为视频没声，PPT这部分也看不出来是想说啥细节，所以只能略过喽

• CNN 边缘检测模型
• 用Transformer做边缘检测
• 语义边缘检测
• 遮挡边缘检测

五、拟合（Fitting）

边缘检测出的边缘是一个底层的特征 low-level
从边缘图中，通过拟合技术，进一步提取需要的几何边缘

1. 拟合的基本概念

（1）目标

找到一个参数化的模型，来表示特征

（2）难点/需要解决的问题

• 噪声：图像以及预处理会存在各种噪声，影响拟合
• 外点/无关点：比如我只想找车上的几何形状，那么车之外的像素点都是无关点，这些点会影响程序自动化寻找车的形状
• 缺失数据——遮挡：由于遮挡关系，几何形状可能是间断的。比如想检测车后面房子的窗户的形状，结果由于车在前面，被挡住了。

2. 拟合的常见方法

（1）最小二乘法（Least squres line fitting）

① 原理

a. 确定目标函数

b. 最小化目标函数

利用$\|\mathbf{P}\|^2 = P_1^2 + P_2^2 + \cdots + P_n^2=\mathbf{P}^T\mathbf{P}$

最终得到了最优直线对应的m和b（B矩阵）

② 缺陷

所以缺陷就是没办法解决垂直线，因为它不是旋转不变的，只要发生旋转了，就解决不好问题了

（2）全最小二乘法（Total least squares）

① 原理

本质上就是将计算的距离从竖直方向距离改为点到直线的距离
最优化的参数从两个（m，b）变为三个（a，b，d）


其中从对d求导到得到d的a、b表示：

$$\sum_{i=1}^{n} (-2ax_i - 2by_i + 2d) = 0$$

$$d=\sum_{i=1}^{n}(ax_i+by_i)$$

$$d = \frac{a}{n} \sum_{i=1}^{n} x_i + \frac{b}{n} \sum_{i=1}^{n} y_i = a \bar{x} + b \bar{y}$$

以及其中矩阵U：

② 优缺点

• 优点：相较于最小二乘，具有旋转不变性
• 缺点：不能很好地对抗噪声点
  

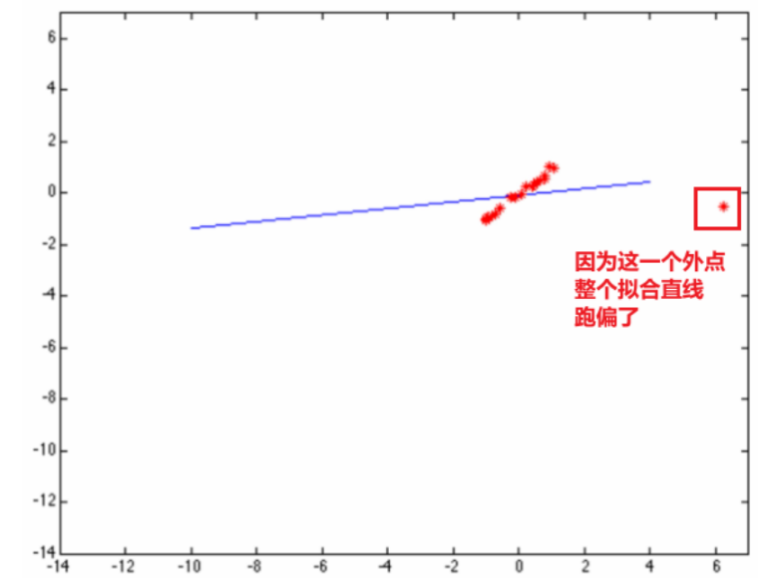
③ 从概率角度理解全最小二乘

感觉不是很重要，但是PPT讲了，就附带一下吧
也就是最小二乘法与极大似然估计之间的内在联系

假设：
存在一条理想直线（最终的拟合直线）$ax+by=d$，法向量$\mathbf{n}=(a,b)$，直线上真实点坐标为$(u,v)$，但观测点$(x,y)$受到垂直于直线方向的噪声干扰。
观测点的表示：

$$(x, y) = (u, v) + \varepsilon \cdot \frac{(a, b)}{\sqrt{a^2 + b^2}}$$

其中$ε$是噪声幅值，服从均值为0、标准差为$σ$的高斯分布
单点概率密度：
给定直线参数 $(a,b,d)$，观测点$(x_i,y_i)$的噪声服从高斯分布，由于理想点$(u,v)$满足$au+bv=d$，垂直距离$\varepsilon = \frac{|ax_i + by_i - d|}{\sqrt{a^2 + b^2}}$，结合高斯分布公式，化简得到观测点$(x_i,y_i)$的概率密度为：

$$P(x_i, y_i \mid a, b, d) \propto \exp \left( -\frac{(ax_i + by_i - d)^2}{2\sigma^2} \right)$$

似然函数：
假设所有观测点独立同分布，联合似然函数为各点概率的乘积：

$$\mathcal{L}(a, b, d) = \prod_{i=1}^{n} \exp \left( -\frac{(ax_i + by_i - d)^2}{2\sigma^2} \right)$$

对数似然函数：

$$\ln \mathcal{L}(a, b, d) = -\frac{1}{2\sigma^2} \sum_{i=1}^{n} (ax_i + by_i - d)^2$$

最大化似然函数相当于：

$$\max_{a,b,d} -\sum_{i=1}^{n} (ax_i + by_i - d)^2$$

等价于全最小二乘的目标：

$$\min_{a,b,d} \sum_{i=1}^{n} (ax_i + by_i - d)^2$$

（3）鲁棒最小二乘法

① 原理

根据点的残差来差异化特征贡献，也就是离得近的贡献大，离得远的贡献小
找到最优参数 $\theta$ 最小化目标损失函数：

$$\sum_{i} \rho(r_i(x_i, \theta); \sigma)=\sum_{i} \rho(u;\sigma)=\sum_{i} \frac{u^2}{\sigma^2+u^2}$$

其中：

• $u=r_i(x_i,θ)$是第 $i$ 个数据点的残差（模型预测值与真实值的偏差）
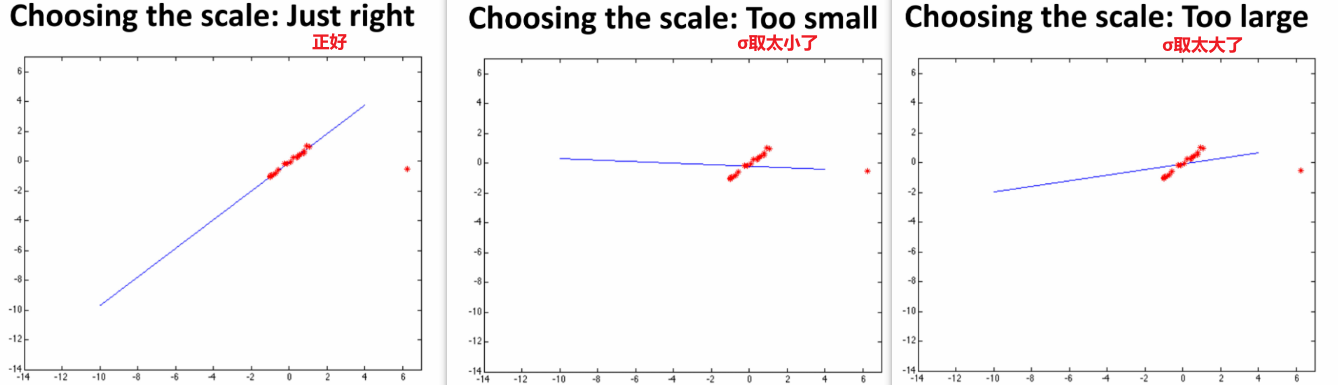
• $σ$ 是尺度参数，控制函数从“类平方”到“饱和”的转折点。$σ$ 越小，函数越早进入饱和区，模型对离群点更鲁棒；$σ$ 越大，饱和区延迟，模型更接近传统最小二乘。
  
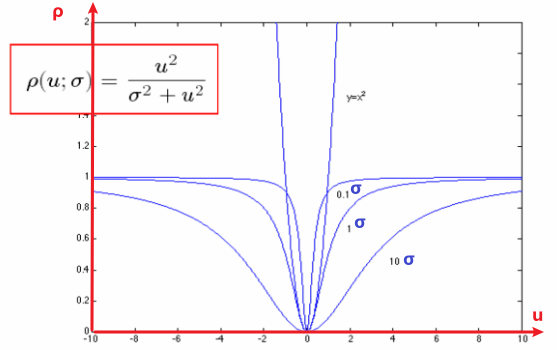
  如上图，横坐标是残差 $u$ ，纵坐标是对应的响应（贡献）$\rho$，三条曲线分别展现了不同 $σ$ 大小带来的影响。

② 特点

• 非线性优化过程，经过了一个非线性的变换
• 可以先用全最小二乘初始化初始解，再用梯度下降方法取求最优解
• 受 $\sigma$ 大小的影响很大，一般选择1.5倍的平均残差

③ 优缺点

• 优点：对外点具有鲁棒性
• 缺点：依赖于 $σ$ 的取值，取大取小都不好；如果外点数变多，表现可能也不是那么好了
  

（4）随机采样一致性算法RANSAC

如果有很多外点，鲁棒最小二乘可能也不好用了
RANSAC：Random sample consensus

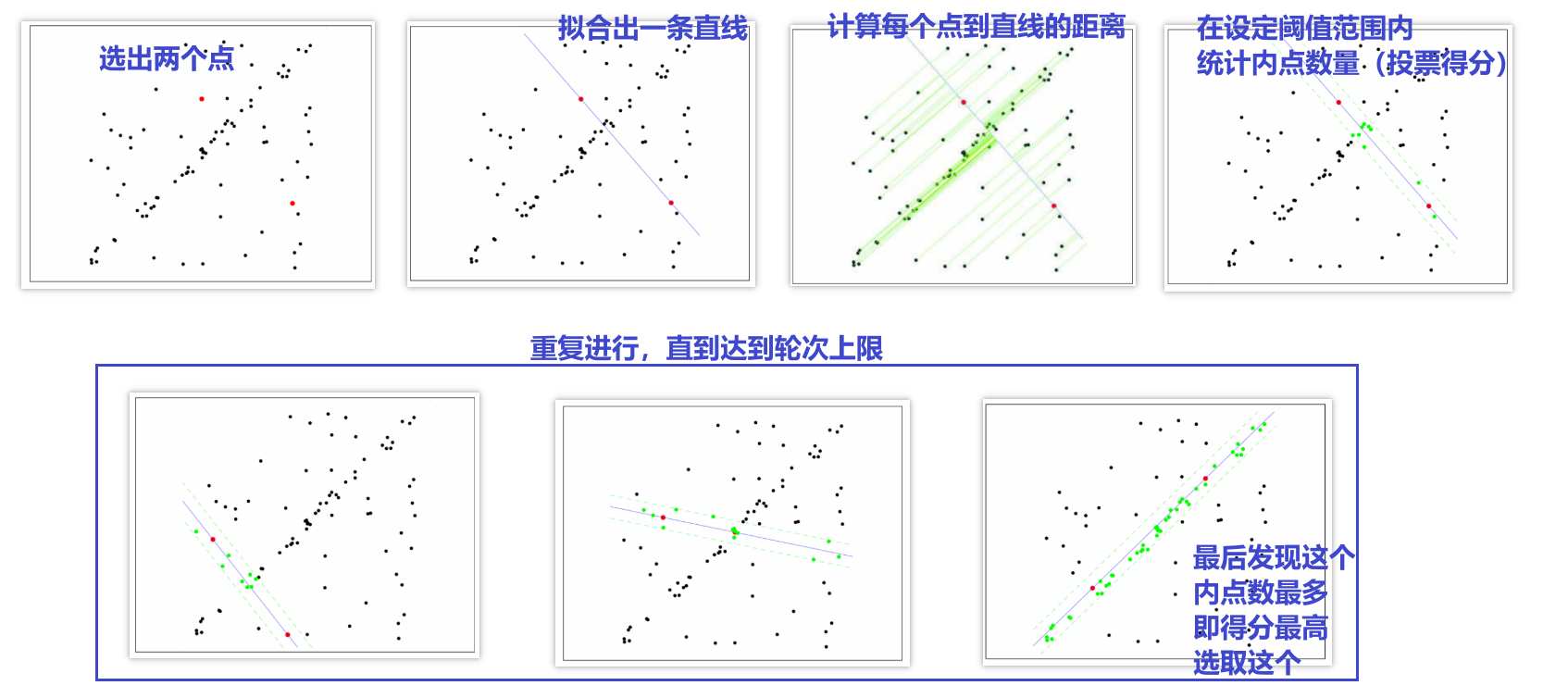
① 原理流程（以直线为例）

a. 随机从所有点中选择所需的最少的样本点（如估计一条直线方程需要两个点，其他模型可能不一样）

b. 拟合出一条直线

c. 计算每个点到该直线的距离，并设置一个距离的阈值/门限

d. 记录落在阈值/门限范围内的点的数量（内点数量），作为投票得分

e. 重复abcd这四步若干次

f. 跳出迭代后，选用内点最多（投票得分最高）的拟合结果

② 参数设置

a. 初始化样本点数 s

这个是跟任务相关的，直线最少需要俩点，其他模型可能更多

b. 门限/阈值 t

c. 迭代次数 N

迭代多少次才结束呢？需要选取一个合适的迭代次数

i. 基本原理

先设置两个概率：

• 最优概率 $p$： 只要这个拟合结果有 $p$ 的概率能够准确检测所有样本点的，那么久接受它，不去继续找了
• 外点概率 $e$： 某个点不属于拟合结果的概率是 $e$

然后进行下面的理解：

• 最终拟合直线的准确率是 $p$
• 最终拟合直线预测错误的概率是 $1-p$
• 外点的概率是 $e$
• 内点的概率是 $1-e$
• 对于某一次迭代，最开始选了 $s$ 个点做初始化，内点的概率是 $(1-e)^s$
• 对于某一次迭代，最开始选了 $s$ 个点做初始化，外点的概率是 $1-(1-e)^s$
• 对于总共 $N$ 次迭代，外点的概率是 $(1-(1-e)^s)^N$

对于理想的拟合直线，它已经是由很多内点投票出来的直线了，它对于这些内点，就相当于是可以预测/检测成功的；那相对应的，如果遇到外点了，那可不就是会预测错误嘛
所以：

$$1-(1-e)^s=1-p$$

满足上式的 $N$ 就是我们想要的，反解出来：

$$N=log(1-p)/log(1-(1-e)^s)$$

ii. 自适应算法

实际的外点概率 $e$ 经常是未知的，如果外点特别多的话，$N$ 会非常大，也不利于计算

步骤如下：
$N=∞,sample\_count=0$
While $N>sample\_count$ :
  选择一个样本并计算内点率 $1-e$（就是正常拟合后算出来阈值内的内点数，然后算个占比）；
  进一步计算出外点率 $e$ （就是1-内点率）
  根据 $N=log(1-p)/log(1-(1-e)^s)$ 更新 $N$
  $sample\_count$++

【其实通过分析公式，可以看出 $e\propto N$，所以上面的自适应算法由于动态计算 $e$，就实现了动态调整 $N$】

d. 一致性 d

比如对于总共有100个点，我们可以设置d=50，迭代结束后：

• 如果所有拟合结果的内点数（投票得分）都没到50，最终给出投票数最高的那个就行
• 如果有多个都到了50，除了最高的以外，这些高于50的也给出来，输出多条直线。
  【因此可以通过设置d来控制结果要多条直线还是单条直线】

③ 优缺点

a. 优点

• 简单、通用
• 适用于许多不同问题
• 在实践中效果通常不错

b. 缺点

• 需要调整的参数很多
• 内点数比较低（外点数比较多）的时候，迭代次数太多
• 初始化不稳定，比如如果第一次外点数就爆多，那很坏了；
  但是如果第一次内点数爆多，那说不定很快就解决了；
  所以这初始化挺不稳定的

④ 补充

• 还是建议记忆一下 $e\propto N$
• 真实应用时，其实需要针对特定问题和情况做更多改进，比如RANSAC最终得到最好的一根线，其实再用最小二乘去拟合这根线周围的点，得到的新直线会更好（细化）
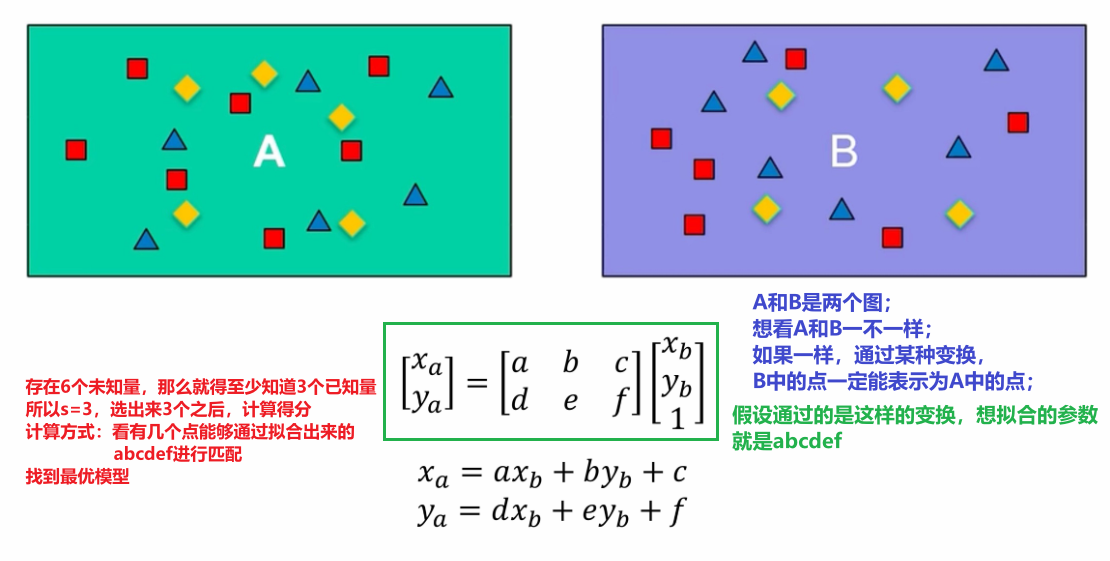
• RANSAC的一个实际应用的抽象示例——指纹匹配
  

（5）霍夫变换

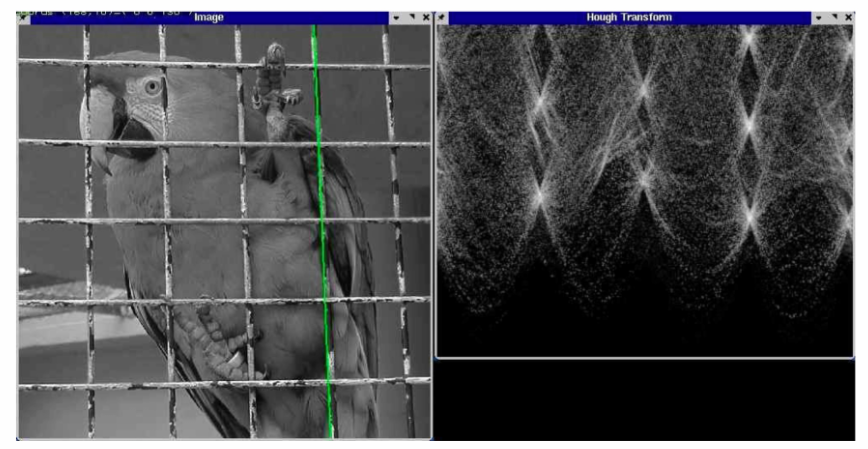
① 引入——RANSAC无法解决的一些问题

如果只想检测下图的绿色直线，那么其他直线都是外点，外电太多了，RANSAC计算量爆炸，效果也受影响。RANSAC不好解决图像中存在大量线的情况

② 霍夫变换需要满足的投票方案

a. 让每个特征为所有与其兼容的模型投票

也就是说，对于一个点，谁能检测到它，它就给谁投票。都各自投完，最后选的模型依然是分数最高的那个。

b, 噪声点不可以一直为同一个模型投票。

不能所有噪声点都投给一个模型，噪声本就是随机产生的，咋可能都投给一个模型，那根本没随机性，不能叫噪声了欸。

c. 只要足够多特征同意一个模型，缺失数据也并不重要（但也不能太多）

只要得分高，有遮挡也无所谓，反正其他大部分特征都选择它了。正因如此，霍夫变换也可以解决遮挡问题。但遮挡的也不能太多，如果几乎全遮挡，剩下零散几个点也没办法确定目标的模型。

③ 霍夫变换的原理

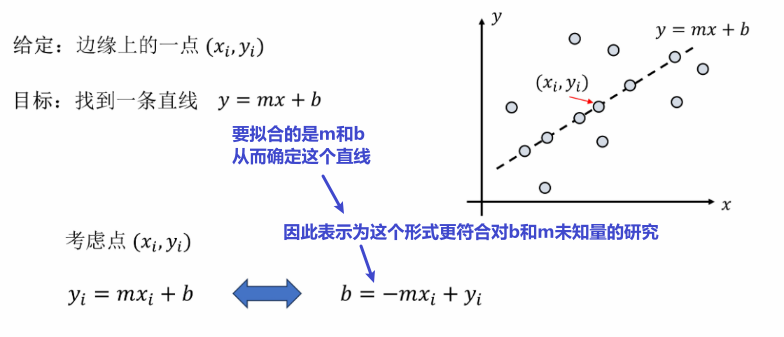
于是可以绘制出图像空间和参数空间：

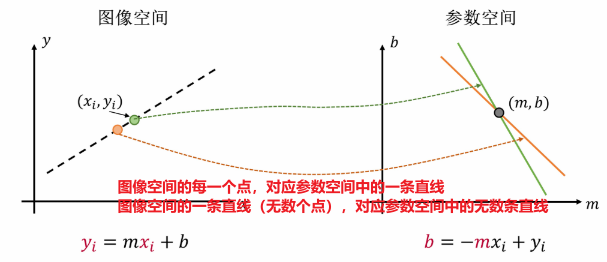
当情况逐渐复杂：

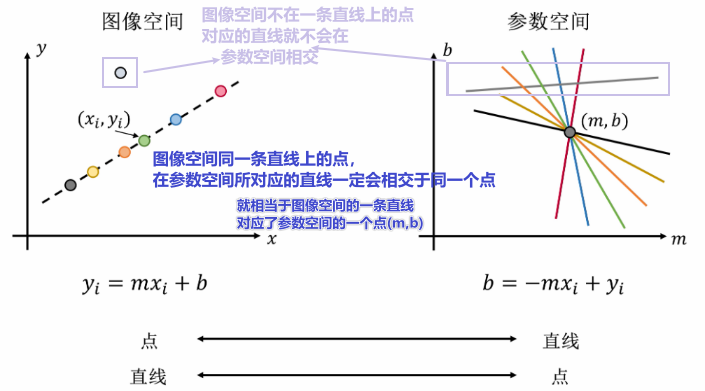
④ 霍夫变换的流程

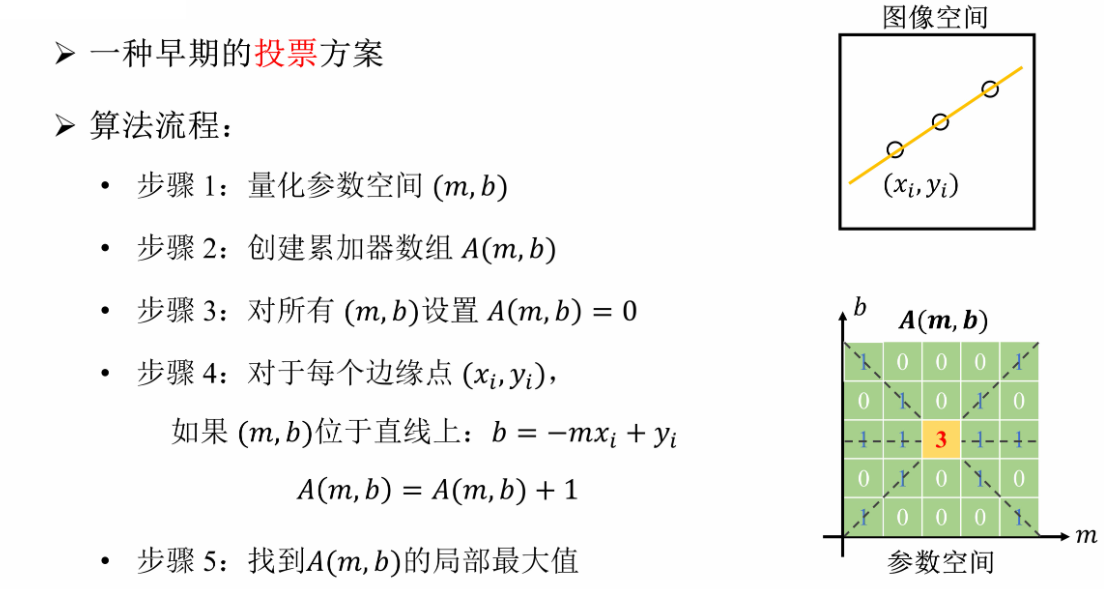
如果图像空间有其他的直线，那么在参数空间就会出现其他的极大值，这个可以在下面的例子中看到

⑤ 霍夫变换的检测示例（数学模型上）

最简单的情况：

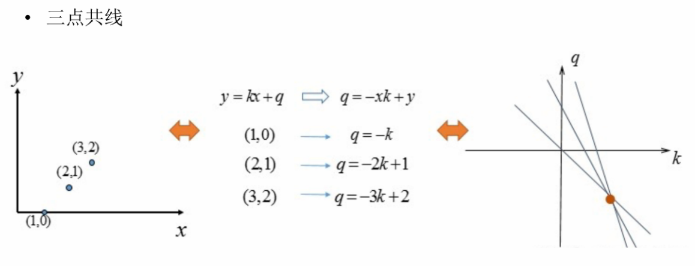
稍微复杂的情况，多个点—多个拟合结果—多个局部极大值

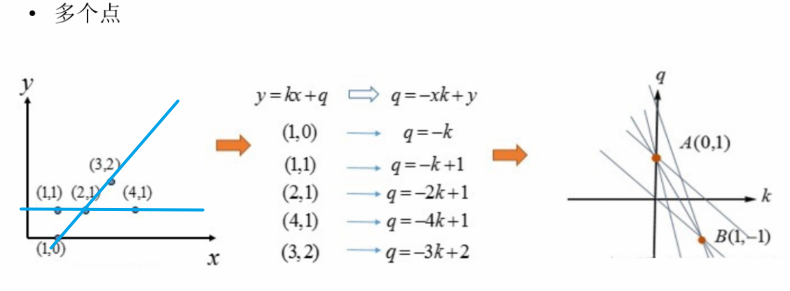
多条线的情况，每条线一个局部最大值：

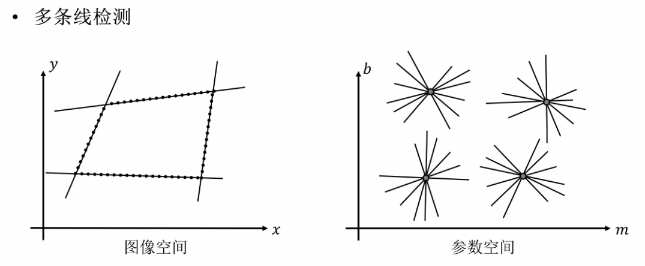
⑥ 传统霍夫变换的局限性

对于垂直的线，没斜率，没法对应到参数空间：

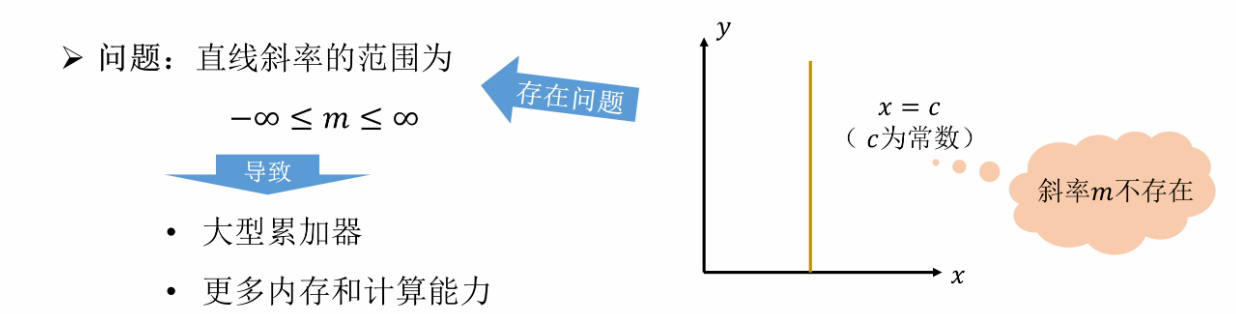
如果累加器设置的太小，那可能没包含我们涉及到的点；
如果累加器设置的太大，那就需要遍历所有斜率，对内存和计算能力要求太高

⑦ 改进：极坐标系下的霍夫变换

a. 原理

改用极坐标系，用 $\theta$ 表示方向，用 $\rho$ 表示原点到直线的距离

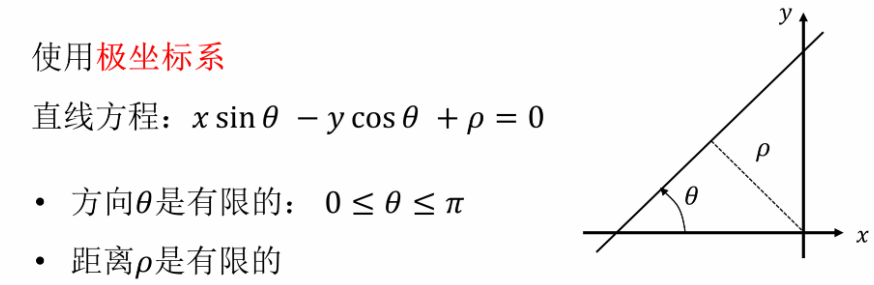
$\theta$ 的范围显而易见；$\rho$ 的范围是因为图像有边界，最大也就是图像对角线的距离

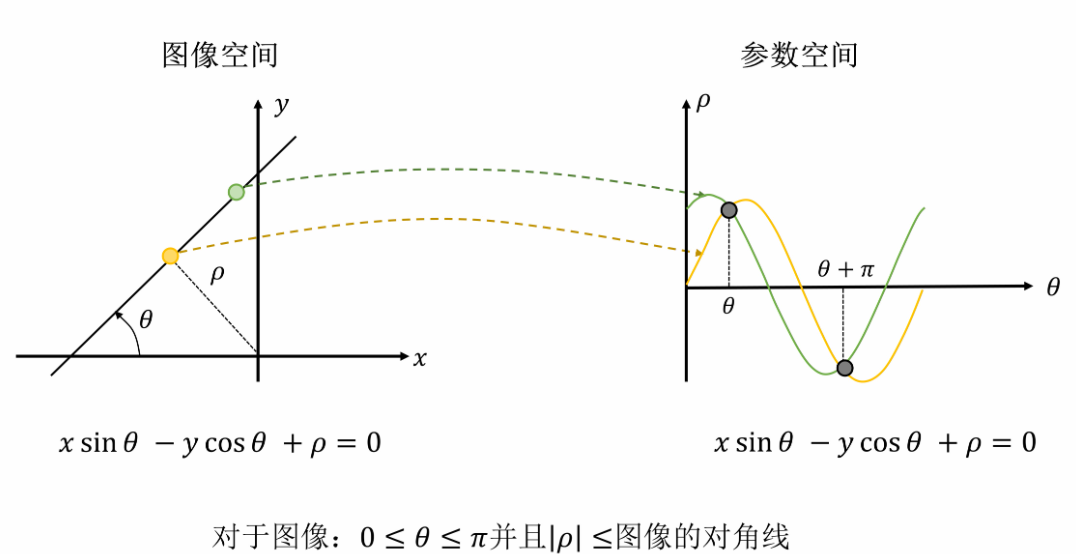
同样可以找到局部极大值

b. 步骤

c. 优点

如上图，$\theta$ 有范围，可以遍历表示垂直的直线

d. 进一步改进提升效率

上图橙色问题是想表明，对于每个角度都遍历，计算量有点大，咋办
解决方案：
可以先用边缘检测，拿到最大梯度方向，而边缘方向和梯度方向是垂直关系，则可以在这个方向（角度）进行极坐标霍夫变换。同时，也可以根据这个角度来设置一个小的范围，更加严谨地进行遍历~

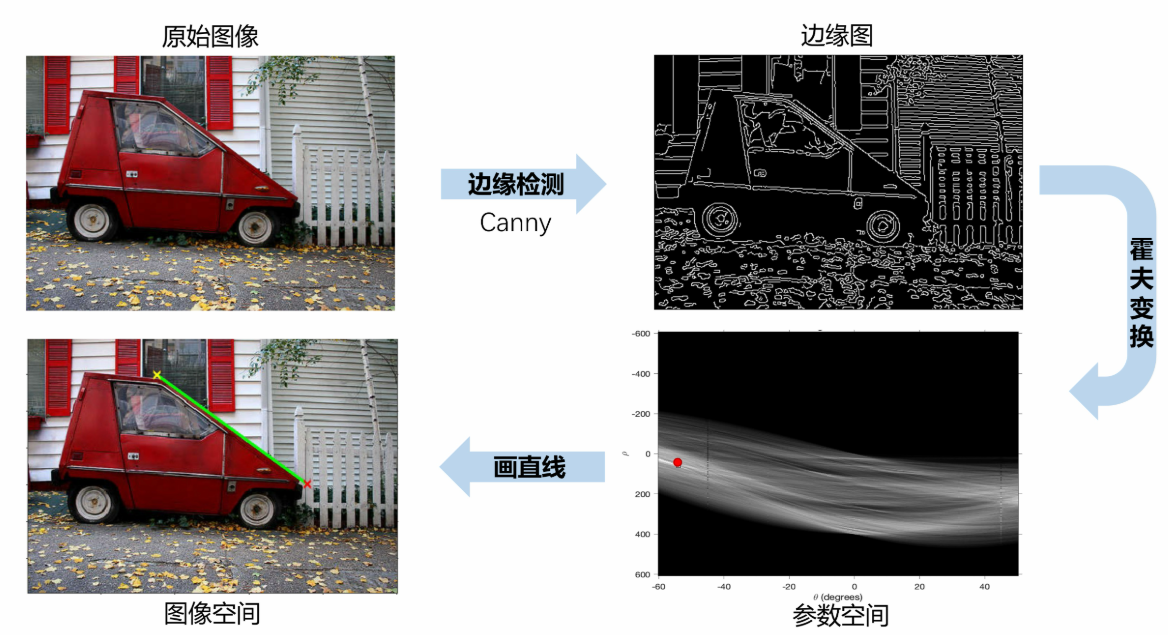
⑧ 霍夫变换的实例效果（实际任务上）

⑨ 霍夫变换的影响因素与解决

a. （自身）噪声的影响

i. 影响

一个例子：

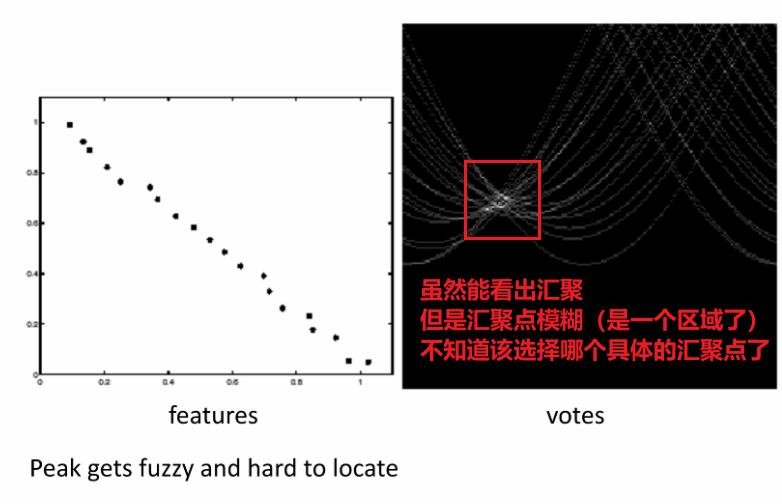
噪声大小和投票数最大值的关系图（以20个点的图为例）：

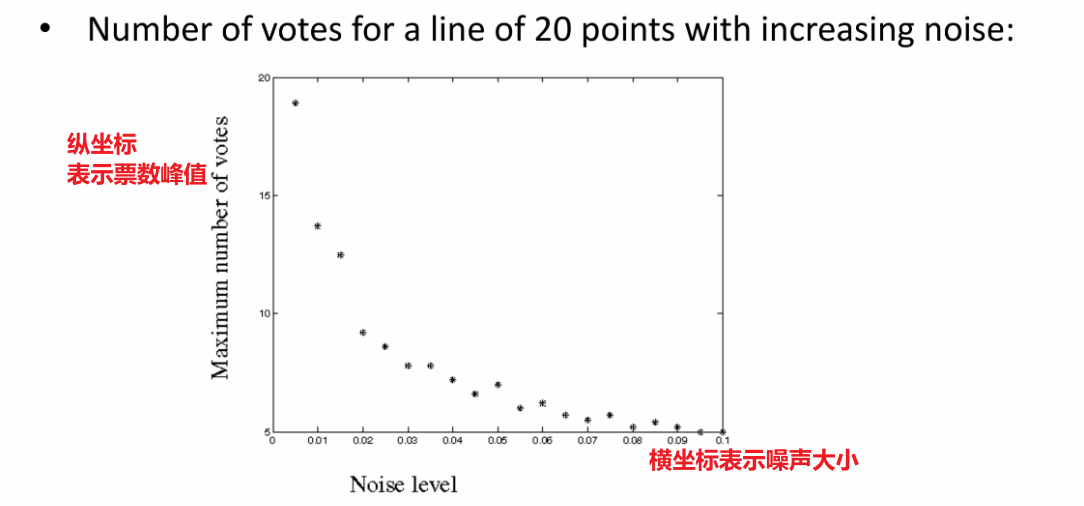
可以看出噪声越大，票数峰值越小，对投票的影响越大
即噪声越大，霍夫变换性能越差

b. （外部噪声）随机点的影响

随机点是外部随机生成的噪声点，和刚才那个自身的噪声不一样，这个是外部随机出现在图像中的随机点。一个是自身的，一个是外部的。

一个例子：

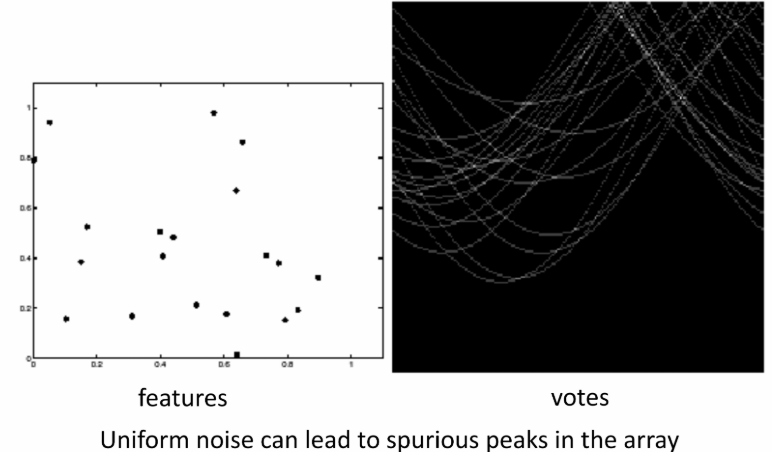
随着随机点噪声的增大，越有可能出现虚假峰值（伪峰值），也就是由这些随机噪声点投票出来了一个结果，而不是我们本来的数据。

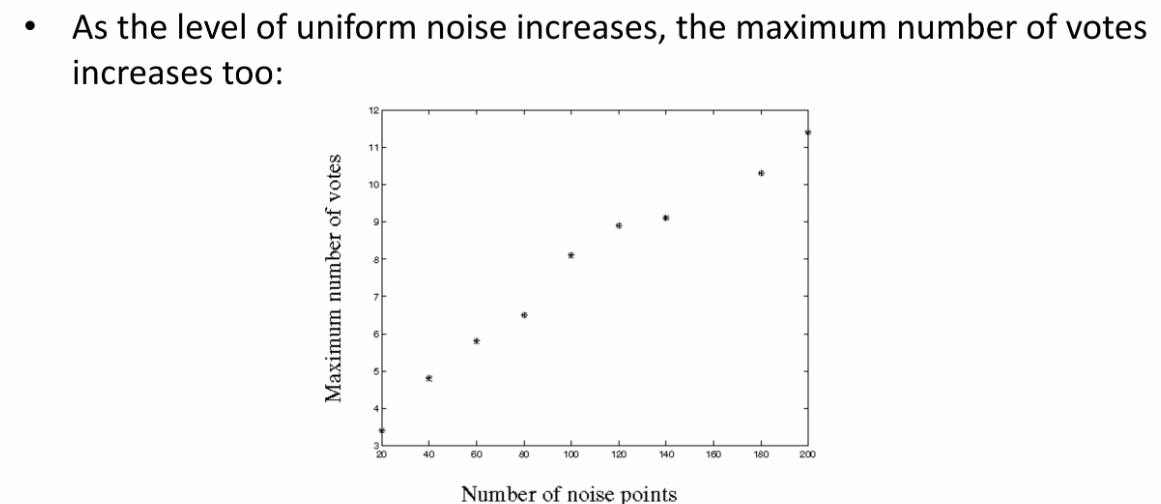
如上图所示，随机点越多，伪峰值越可能出现。

c. 解决

• 方法1：在对参数空间进行离散化时，选取一个合适大小的网格
  不能太大，也不能太小
  
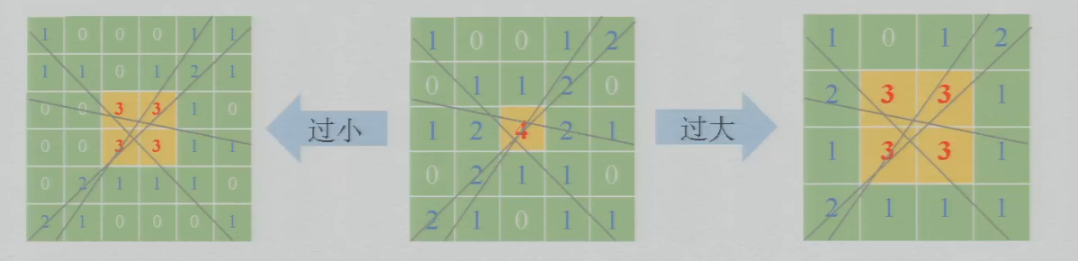
• 方法2：软投票——不采用“落在某个格子”来投票，而用“距离”来投票
  相当于一票掰开好多份，给近的多些，给远的少些
• 方法3：尝试去掉不相关的特征，只选择具有明显梯度的边缘做霍夫变换

⑩ 霍夫变换检测圆形

a. 原理

圆的方程：$(x-u)^2+(y-v)^2=r^2$，其中 $(u,v)$ 是圆心，$r$ 是半径
一个圆由三个参数确定：$u,v,r$
依旧是从图像空间变换到参数空间
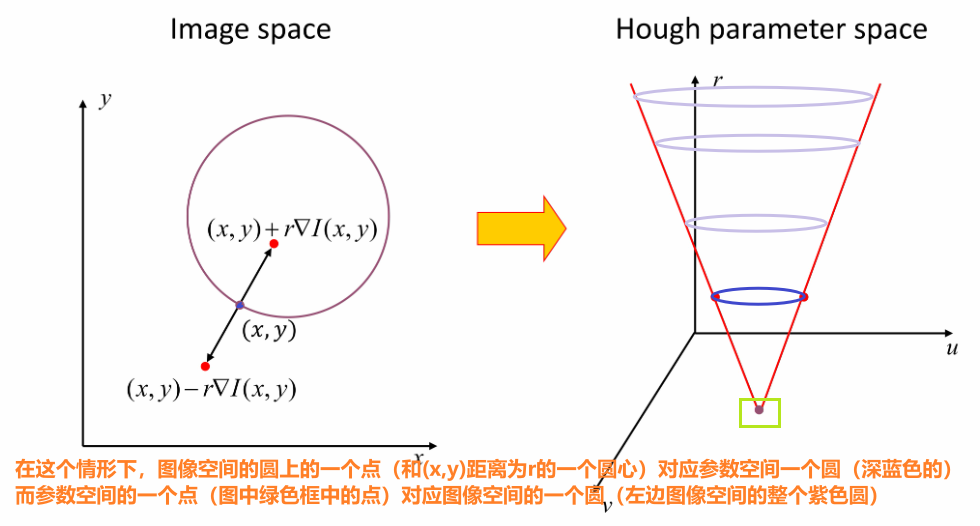
读懂下面的图，需要先进行以下理解：

• 图像空间的一个圆，可以用三个参数表示：圆心坐标 $(x, y)$ 和半径 $r$ 。所以，图像中一个圆，可以用三维参数空间中一个点来表示
• 一个点如果在图像中的某个圆上，那它和圆心所成的方向，是该点图像梯度的方向
• 已知的某点图像梯度方向，经过图像中某一个点的所有可能的圆，可以在x,y,r三维空间中用两根直线表示。
  （如果不考虑该点梯度方向，则笛卡尔坐标系中某一个点，其所有可能的圆，在参数空间中可以用一个立体圆锥曲面表示！）
• 对于图像中某个像素点 $(x,y)$ ，当给定 $r$ 半径值后，仅有两个可能的圆心位置（这两个潜在可能的圆心位置相对这个像素点互为镜像位置），这两个圆心的位置可以通过x，y，r，以及图像梯度角度值计算出来。
  

⑪ 广义霍夫变换

a. 动机

普通霍夫变换需要用方程描述要检测的形状，从而获得图像空间到参数空间的变换，但有些形状很难用方程参数化描述

拟合无法用方程描述的形状

b. 原理

我们的目的：找到一个能表示这个形状的参考点，最终模型可以表示这个参考点
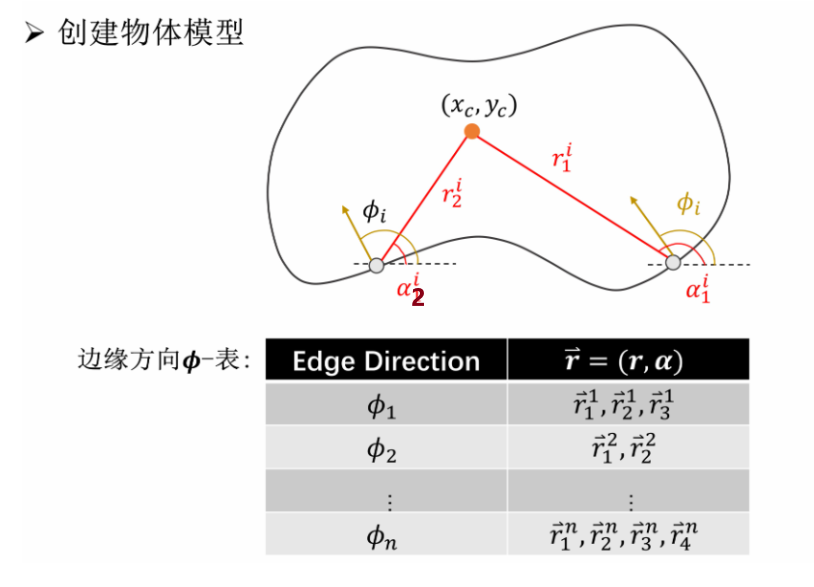
例如下图的不规则形状，怎么做：

• 先假设参考点是 $(x_c,y_c)$，这个参考点的具体坐标我们不知道，只是先设出来。
• 然后对于边缘上的所有点，每个点都要计算：
  • $r$ ：点到参考点的距离
  • $\alpha$：点和参考点连线与水平方向的夹角
  • $\phi$ ：点的梯度方向（注意图中说的边缘方向实际上是想说边缘梯度方向）
• 统计梯度方向的投票情况。如图中的 $\phi_i$，可以看出多个点可能存在相同的梯度方向
• 取出投每个梯度方向，拿到各自所包含的点，进行投票。
  

c. 流程

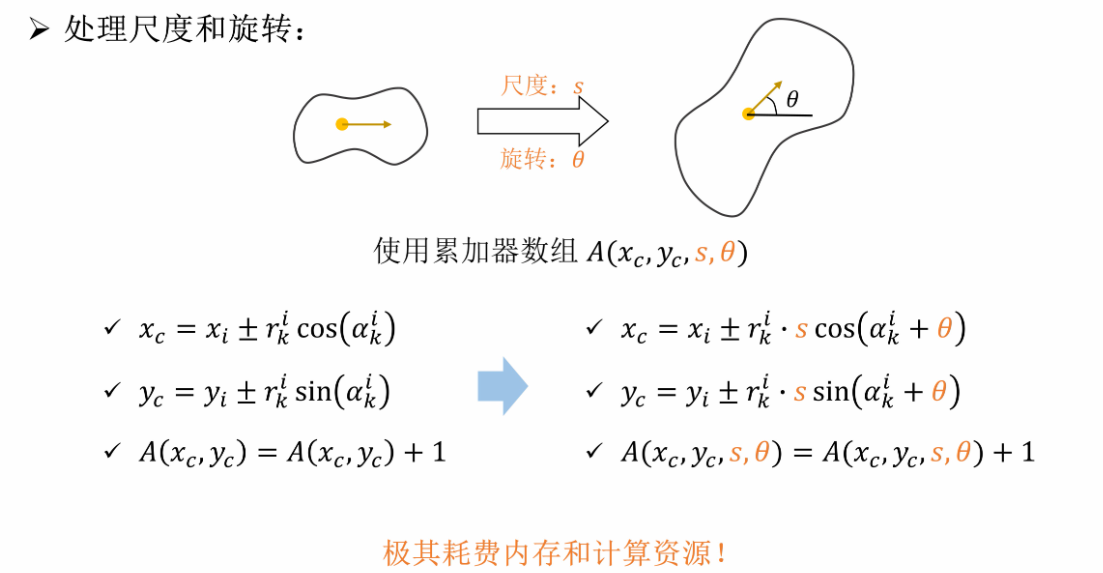
d. 改进

存在问题：无法应对旋转

改进方式：引入更多参数

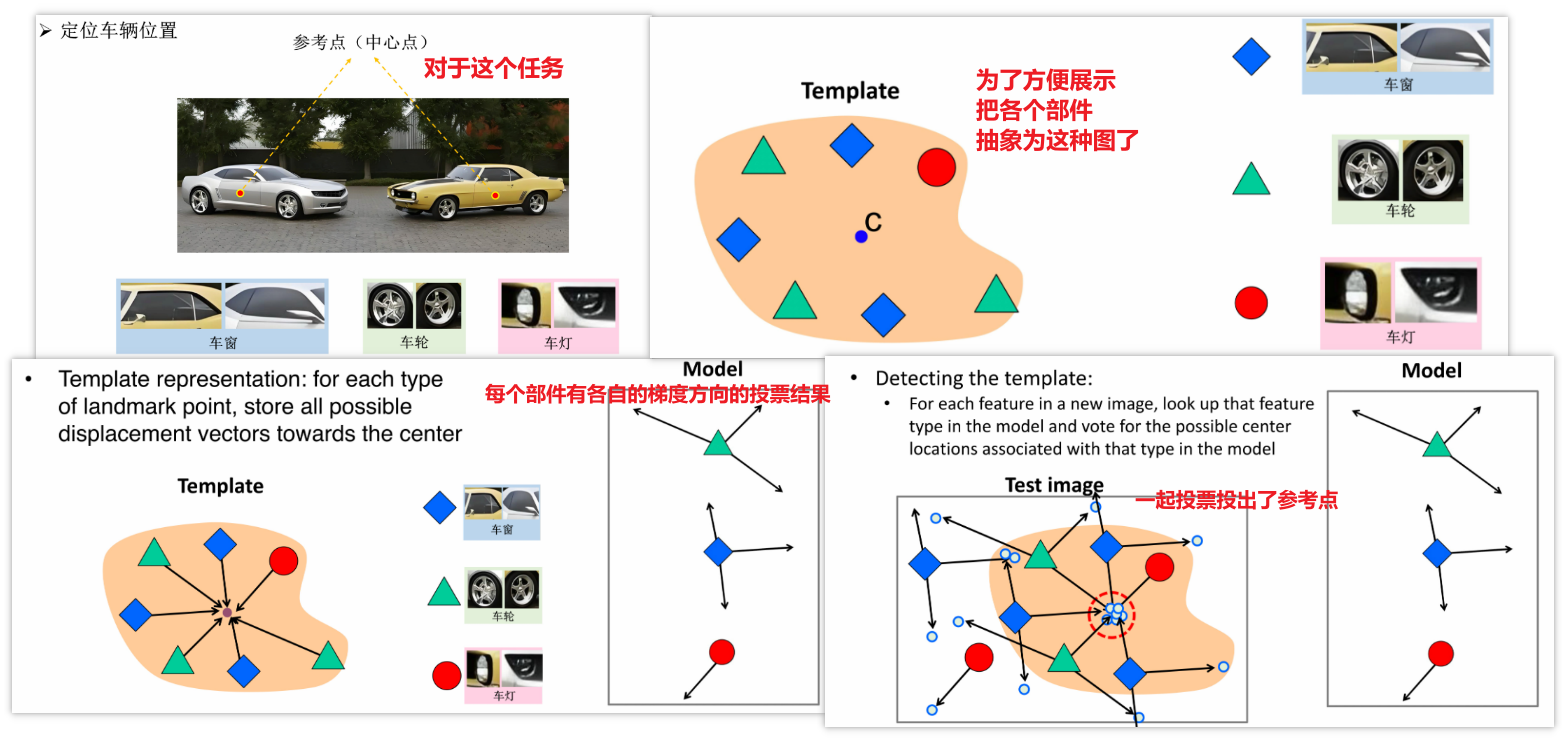
e. 应用

除了检测形状以外，还可以通过检测一些大物体的局部组件相对大物体的位置关系，通过方向投票机制，去锁定图像中某大物体的中心位置。

⑫ 霍夫变换的优缺点

a. 优点

• 可以处理非局部性的（全局的）和遮挡的情况
• 可以检测出多个模型的实例（就是拟合出多个符合要求的模型出来）
• 对噪声比较鲁棒（这是前提条件了，见第②部分）

b. 缺点

• 随着模型参数的增加，搜索空间变越来越大，搜索时间复杂度指数级增长
• 非形状目标可能会在参数空间中产生虚假峰值（伪峰值）
• 很难选择一个合适的网格大小（见⑨.c）

3. 拟合方法的选择

六、局部特征

1. 角点检测

（1）为什么要提取特征

动机：全景拼接

摄像机视角有限，因此需要转动在多视角进行拍摄，完成全景图像。

a. 流程

提取特征 --> 进行特征匹配 --> 根据匹配得到的联系，拼接图像

b. 良好特征的性质（提取哪些特征才更适配任务）

• 可重复性：在几幅图像中可以找到的共同特征
• 显著性：显著区别于其他的特征
• 紧凑性和效率：希望特征能比图像像素少得多，从而计算是高效的
• 局部性：特征只跟其周围的图像有关系（在图像中占据相对较小的区域），对杂乱和遮挡具有鲁棒性

c. 特征点的应用

图像对齐、3D重建、运动跟踪、机器人导航、索引和数据库检索、物体识别…

（2）角点

① 角点的定义

图像梯度在两个方向或更多方向上发生了突变的地方

② 角点的性质

角点具有可重复性、显著性、紧凑性（时间计算效率高）、局部性

③ 判断是否是角点

a. 直观描述

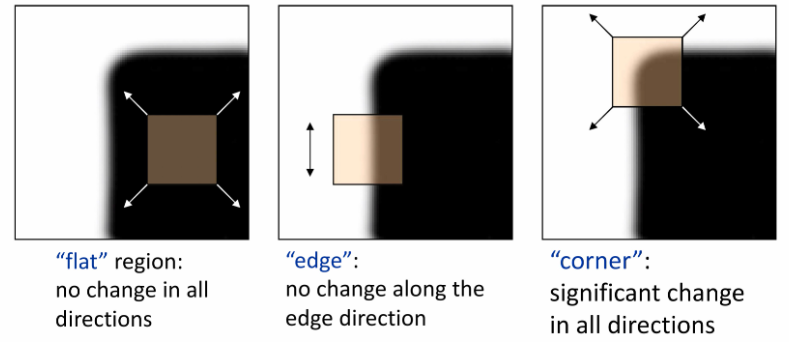
如果是角点，窗口至少沿着两个方向移动会发生变化

b. 数值描述

$E(u, v) = \sum_{x, y} w(x, y) \left[ I(x + u, y + v) - I(x, y) \right]^2$

• $u,v$：平移量
• $I(x,y)$：没有移动前的图像强度
• $I(x+u,y+v)$：移动后的图像强度
• $E(u,v)$：窗口移动前后像素值的差异；
• $w(x,y)$：权值，可根据每个点对整个E(u,v)的贡献的差异特异化设置

i. 将E(u,v)进行二阶泰勒展开，以观测在很小的移动下E(u,v)的数值表现（E(u,v)和u,v的关系会更加直观）：

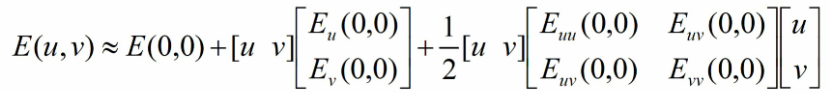
ii. 计算上式中涉及到的偏导数：

iii. 代入数值并整理得到最终二阶泰勒展开式化简结果：

iv. 理解M矩阵：

• 假设窗口检测到的信号是垂直关系的，则有 $I_x I_y = 0$，则M可以转化成下图特征值的形式：
  
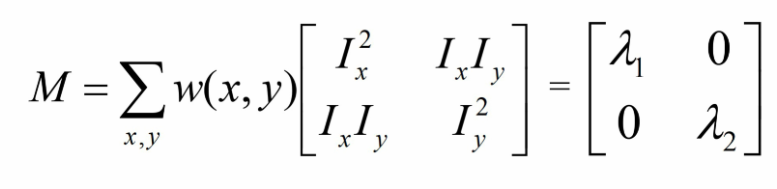
• • 如果点位于垂直的边缘，即 $I_x≠0，I_y =0$ ：
    则 $M = \begin{bmatrix}\lambda_1 & 0 \\0 & 0\end{bmatrix}，E(u,v)=λ_1u^2$
    则 $u$变，$E(u,v)$变；$v$变，$E(u,v)$不变
• • 如果点位于水平的边缘，即 $I_x=0，I_y ≠0$ ：
    则 $M = \begin{bmatrix}\ 0& 0 \\0 & \lambda_2\end{bmatrix}，E(u,v)=λ_2v^2$
    则 $u$变，$E(u,v)$不变；$v$变，$E(u,v)$变

所以，只有 $λ_1$ 和 $λ_2$ 都不为0（或接近0）时，角点才存在

• 假设窗口检测到的信号存在旋转，则M是一个实对称矩阵：
  $M = \begin{bmatrix} a & c \\c & a\end{bmatrix}，c≠0$，
  则可以进行对角化：$M = R^{-1}\begin{bmatrix}\lambda_1 & 0 \\0 & \lambda_2\end{bmatrix}R, R$是一个正交矩阵
  同样等于$M = R^{T}\begin{bmatrix}\lambda_1 & 0 \\0 & \lambda_2\end{bmatrix}R$

所以，无论是否存在旋转，都可以通过上述方法只分析 $λ_1$ 和 $λ_2$ ‘
v. E(u,v)在数学上是椭圆

• 课程中，首先是针对$I_x≠0，I_y =0$ 的情况，进行化简发现$E(u,v)$满足椭圆方程，是一个正椭圆，而刚才第四部分对M的讨论的第二种情况，存在旋转，即一个旋转的椭圆。
• 在形式上，椭圆的轴长由 $λ_1$ 和 $λ_2$确定，方向由$R$确定
• $λ_1$ 和 $λ_2$ 越大，轴越短 ； $λ_1$ 和 $λ_2$ 越小，轴越长
  

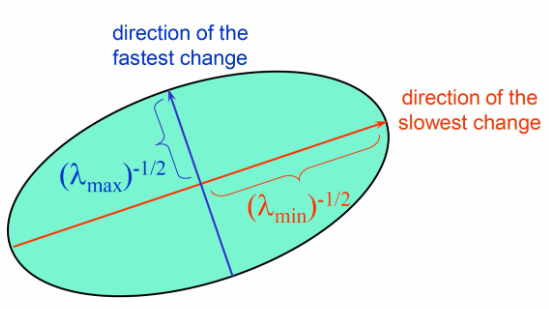
vi. 二阶矩矩阵M的可视化

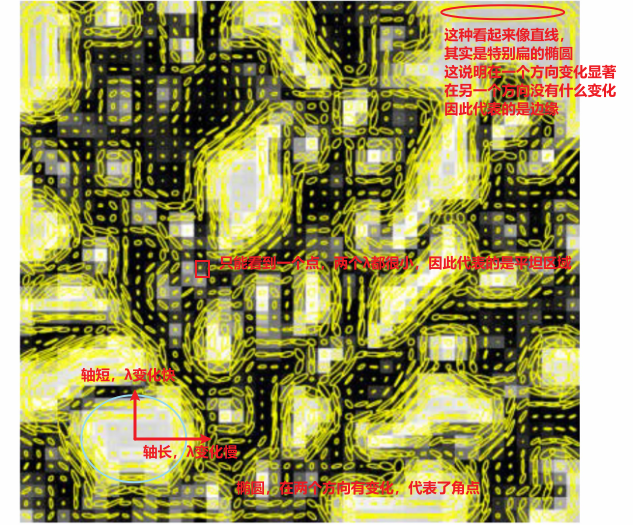
vii. 阶段总结

• $λ_1=0$ 或 $λ_2=0$ ，点在边
• $λ_1≠0$ 且 $λ_2≠0$ 且都非常大，角点
• $λ_1=0$ 且 $λ_2=0$ 或都非常小，平坦区域

viii. 阈值R
Q：多大算非常大？这不方便人工设定
A：$R = \det(M) - \alpha \, (\mathrm{tr}(M))^2 = \lambda_1 \lambda_2 - \alpha (\lambda_1 + \lambda_2)^2$
其中 $tr(M)$ 是矩阵的迹，是主对角线元素之和
$R>0$，则是角点
$R<0$，则是边缘
$R→0$，则是平坦区域

c. Harris角点检测

Harris角点检测就是上面的数值描述方法，总结一下：

• 先在每个像素处计算高斯导数，也就是$I_x$和$I_y$，相关计算见b.ii
• 然后计算每个像素周围高斯窗口的二阶矩矩阵M，相关计算见b.iii
• 然后计算角点响应函数R，相关计算见b.viii
• 将R作为阈值来判断是否是角点，相关判断见b.viii
• 最后进行非极大值抑制，找到响应函数的局部最大值

最后一步的是因为：某一个点是角点（响应较高）时，周围的点可能也是如此。找到最高的即可。

（3）Harris角点的特性

① 好的特征具备的四个特性

可重复性、显著性、计算高效（紧凑性）、局部性

② Invariance 和 Covariance 的区别

• Invariance：$F(I)=F[T(I)]$
  即图像变化前后，用同一个特征提取器$F$提取到的特征是相同的
• Covariance：$F(I)≠F[T(I)]$，但$T'[F(I)]=F[T(I)]$
  即对原始图像提取的特征做变换后，与变换后的图像提取到的特征是相同的

所以，好的特征应当具备Invariance特性，实在不行，Covariance特性也可以

③ 探究Harris角点是否具有Invariance/Covariance特性

a. 对图像强度进行变化

加光照，$I → I+b$，并不改变梯度变化，对$M$矩阵无影响，因此还能检测到角点，满足Invariance

b, 对图像进行尺度变化（缩放）

缩放，$I → αI$，可能将原本低于$R$阈值的响应点也检测为角点，不满足Invariance和Covariance，如图：

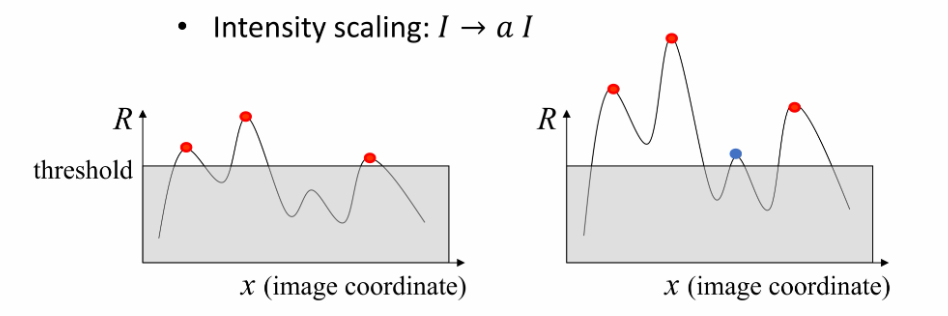
c, 对图像进行平移或旋转

平移或旋转不改变梯度，还是能够检测到角点，但平移或旋转前后提取到的特征不相同，不满足Invariance；但把平移后得到的特征再变化，就相同了，满足Covariance

d. 结论

Harris角点检测对于仿射变换具有部分的不变性
Harris角点检测不具备尺度不变性
如果相机和场景距离固定（图像尺度不变），Harris角点检测可行，反之不可行

---

2. Blob检测

Blob检测具有尺度不变性，而Harris角点检测不具备尺度不变性

（1）Blob（斑点）

① 定义：

二维图像跟周围有着明显颜色和灰度变化的区域

斑点可以是一个区域，但角点只是一个点，因此斑点具有更好的稳定性和抗干扰能力

② 斑点的尺度寻找

找到一个函数，从而自适应尺度的变化，因此有尺度不变性

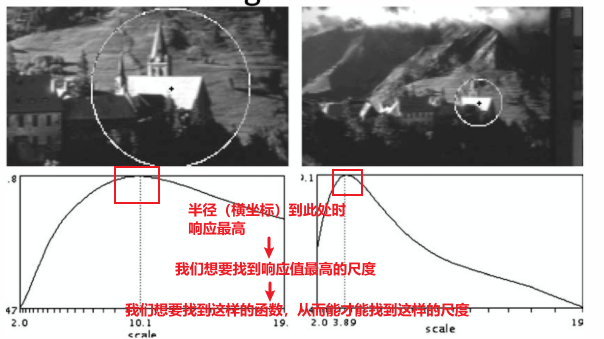
回顾边缘检测

a. 高斯一阶偏导核

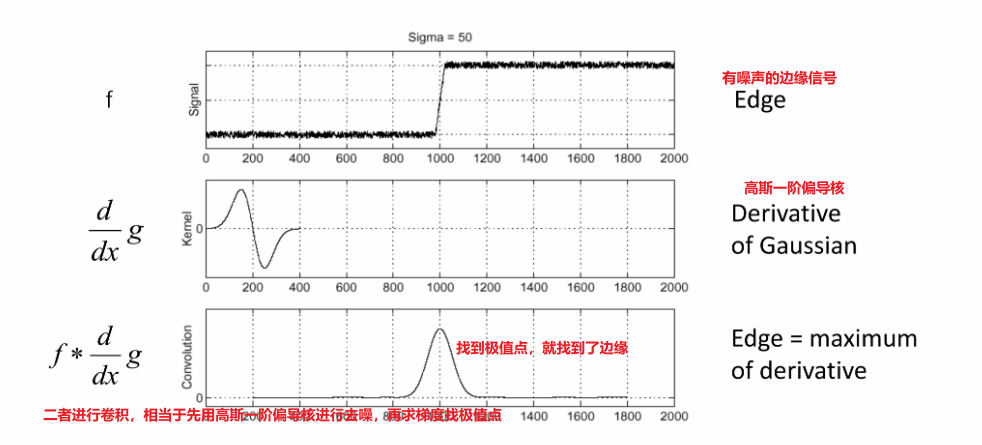
b. 高斯二阶偏导核（拉普拉斯核）

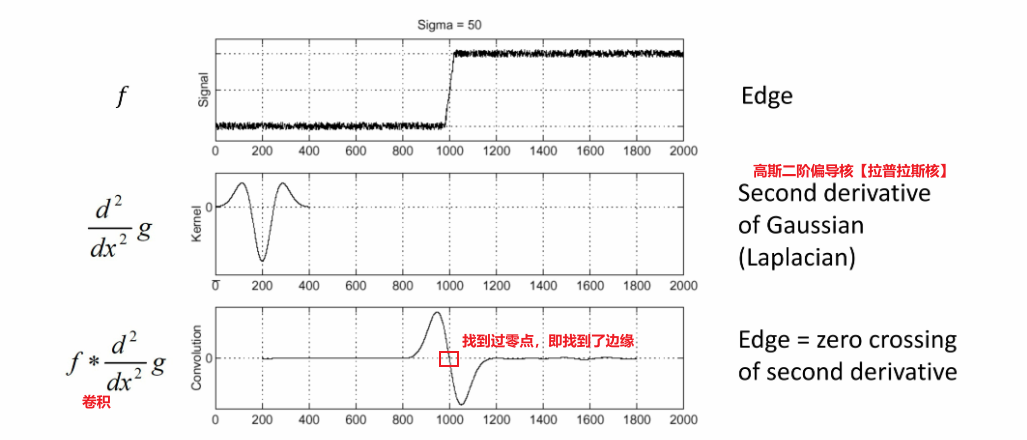
c. 通过拉普拉斯核找到最优尺度

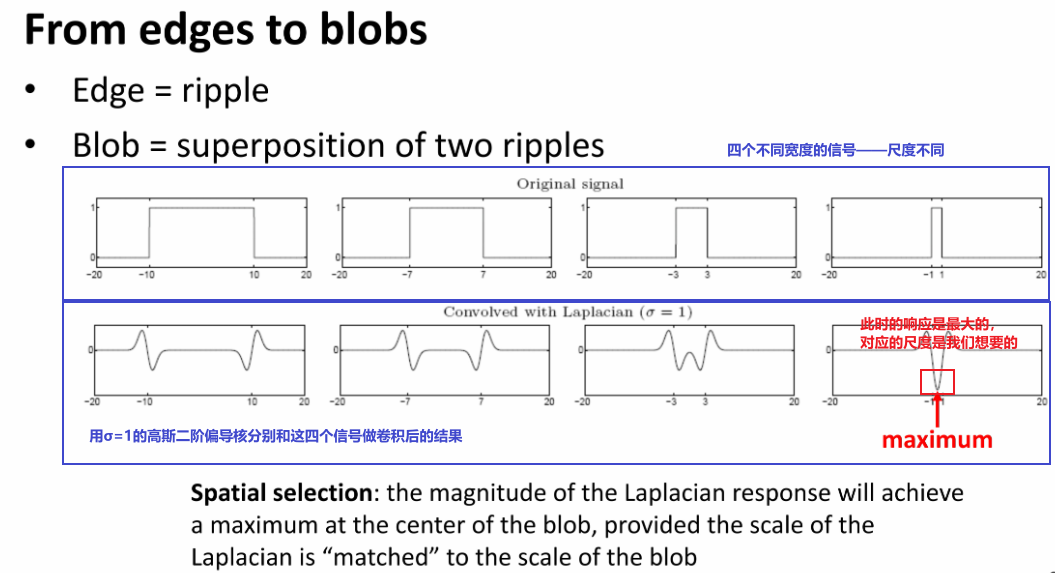
在实际应用中，由于不知道信号长什么样，会设置多个不同方差的拉普拉斯核去卷积，从而才能选择到最好的。

d. 拉普拉斯核方差的选择

问题：随着方差$σ$逐渐变大，信号会逐渐衰减，很难找到极值点
原因：

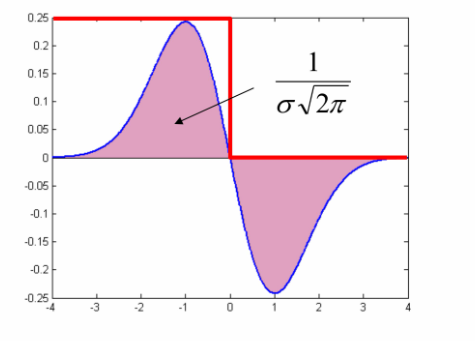
• 数学理解：$σ$越大，图中面积越小，产生出的信号相应越小。（图中仅是高斯一阶偏导核，而二阶会受到更强烈的影响）
• 物理理解：高斯核去噪，$σ$越大，去噪效果越强，把高频信号都去掉了，原本响应值突出的区域也都因此变得平坦了

解决：需要对信号进行补偿，给拉普拉斯核乘上一个$σ^2$：$\nabla^2_{\text{norm}} g = \sigma^2 \left( \frac{\partial^2 g}{\partial x^2} + \frac{\partial^2 g}{\partial y^2} \right)$
从而把分母上的$σ^2$约掉，效果如图，可以找到我们想要的函数曲线了：

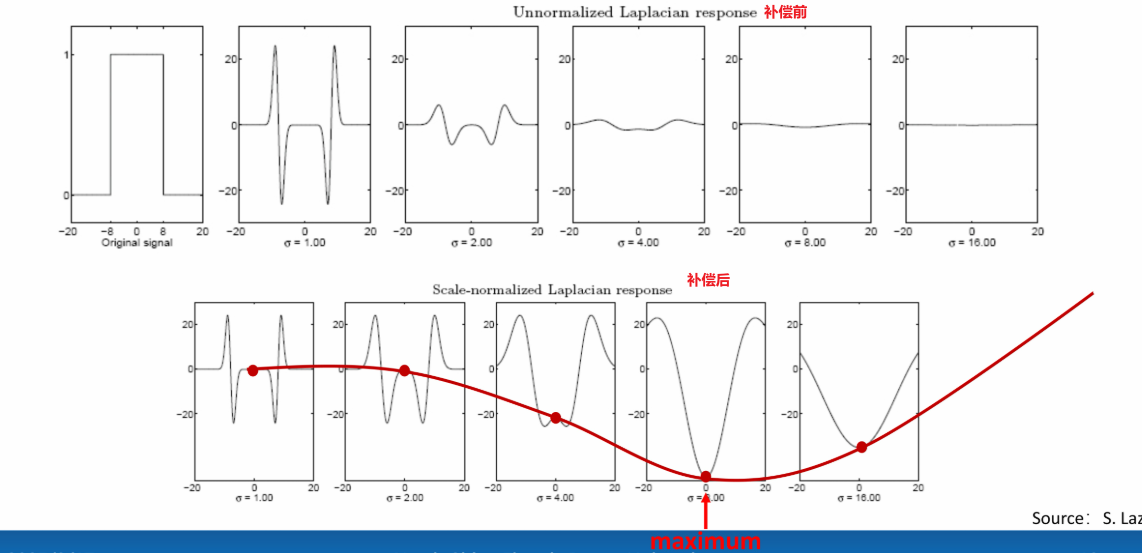
横轴是方差变化，也就是尺度变化；纵轴是响应值变化

e. 拉普拉斯核方差和信号半径的关系

当拉普拉斯核的过零点的宽度和信号的直径恰好相等时，响应值最大

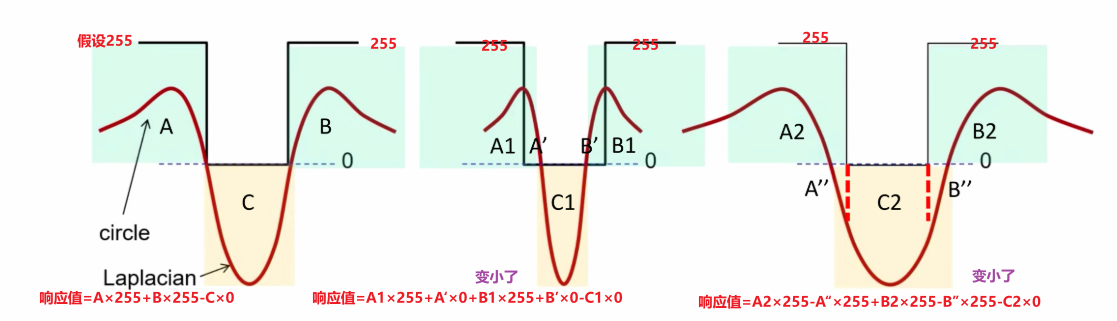
此时也存在关系： $r=\sqrt{2}σ$
这个的计算方式就是让拉普拉斯核等于0（过零点），结合本身斑点存在的关系 $x^2+y^2=r^2$（圆），化简得到了。

大方差，大窗宽，检测大信号；小方差，小窗宽，检测小信号

f, 斑点检测的非极大值抑制

由于检测时，相邻区域的点可能响应值都很大，因此步骤：

• 取下图三个尺度的27个点的响应值
• 对最大响应值对应的点，作为圆心，根据对应尺度和计算出的半径画圆
  
  （此图假设检测模板是3×3的，同时在实际检测中一般仅比较相邻三个的尺度如图所示）

③ 斑点检测计算量大的解决办法

a. 和Harris角点检测相结合

• 先用Harris角点检测，把角点检测出来
• 在每个角点周围，建立一个尺度空间，看周围有没有合适尺度（斑点检测画圆）

b. SIFT特征

见下

（2）SIFT

① 高斯差分

a. 定义

两个高斯核做差

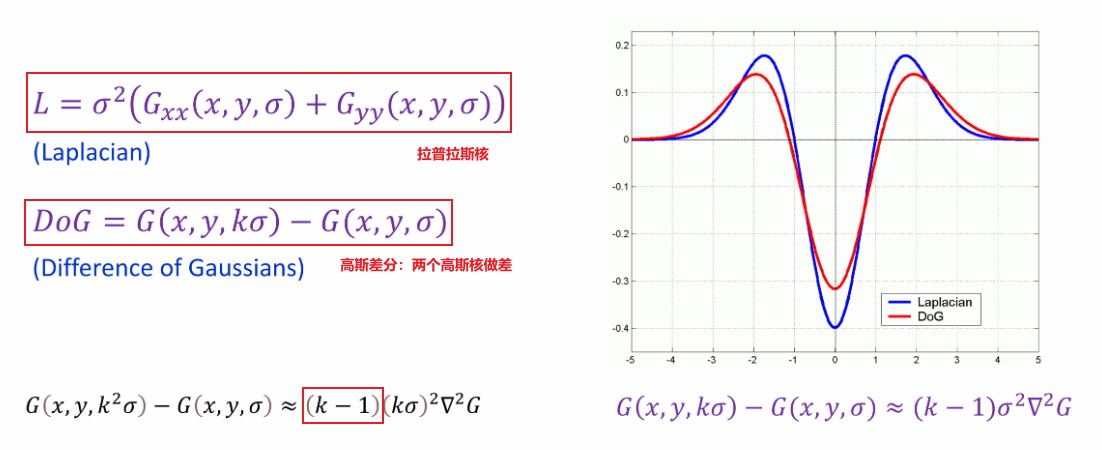
b. 优势——效率提升方式

• 高斯差分和拉普拉斯之间就差了一个常数：$k-1$，则：高斯函数→高斯差分→拉普拉斯
  
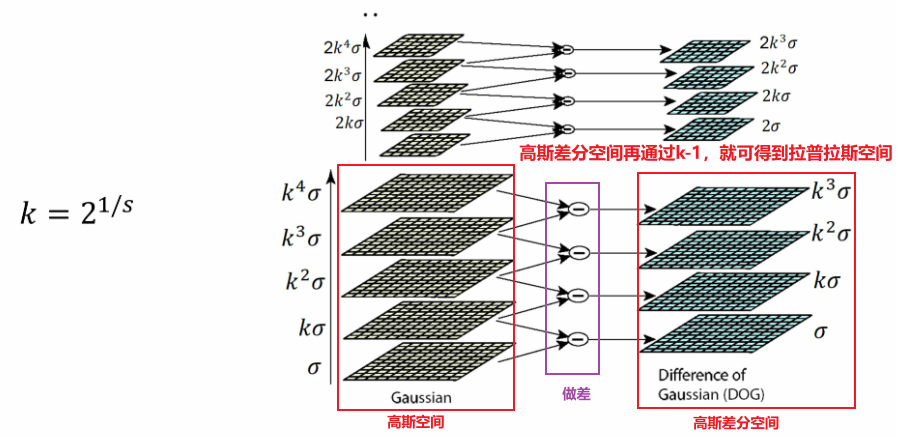
  （图中这样一组空间成为一个Octave——八度）
• 在构建高斯空间时，可以利用”过两个小的等于过一个大的，关系是$\sqrt2$ 的性质，来得到其他尺度的高斯层 【Octave组内加速】
• 如果不想用大方差的拉普拉斯核和大信号做卷积，可以通过：
  先把图像进行缩放，用小方差的卷积核与缩放后的图像做卷积，找到的尺度空间再乘回缩放倍数
  这样可以避免一直增大卷积核的方差不断做卷积构成新的Octave，直接用原来的小方差卷积核就可以构建新的Octave了
  所以在实际应用中，对于1-8的尺度，可以：尺度为1-2时，用原图计算；2-4时，用1/2原图计算；4-8时，用1/4原图计算。拼起来就可以得到连续的尺度空间。
  【Octave组间加速】

c. 如何设置k的数值

$k=2^{1/S}$，因为只有满足这个关系才能构建连续的尺度空间
S是怎么来的：

• 对于5层高斯空间，有4层高斯差分空间，则有4层拉普拉斯空间，我们在前面说过，一般仅比较相邻三个的尺度，则有两种可能，S=2（123、234两种可能）
• 对于6层高斯空间，同理，则有三种可能，S=3（123、234、345三种可能）

② SIFT特征的特性

a. 拉普拉斯相应的Invariance

当图像进行旋转或缩放时，拉普拉斯算子计算出的响应值不会改变。

b. 斑点位置和尺度的Covariance

当图像进行旋转或缩放时，检测到的“blob”的位置和尺度会相应地变化。

c. 对于强度、角度、形状变化不满足Invariance和Covariance

角度和形变的解决方案：经过大小归一化变成椭圆，再利用梯度方向直方图按梯度最强方向进行旋转（梯度方向直方图见下）
强度（光照）变化的解决方案：SIFT描述子投票（SIFT描述子见下）

大小归一化：计算出M矩阵，微调$λ_1$和$λ_2$，把小的变大一点，迭代微调，直到$λ_1$和$λ_2$相等，相当于接近于原始的正圆了
【不确定理解的是否正确，老师在这里的讲解逻辑很混乱，讲的不太好这里】

③ 梯度方向直方图

梯度强度：$\sqrt{I_x^2+I_y^2}$
梯度方向：$arctan\sqrt{I_x^2+I_y^2}$
箭头方向表示梯度方向，箭头长度表示梯度强度

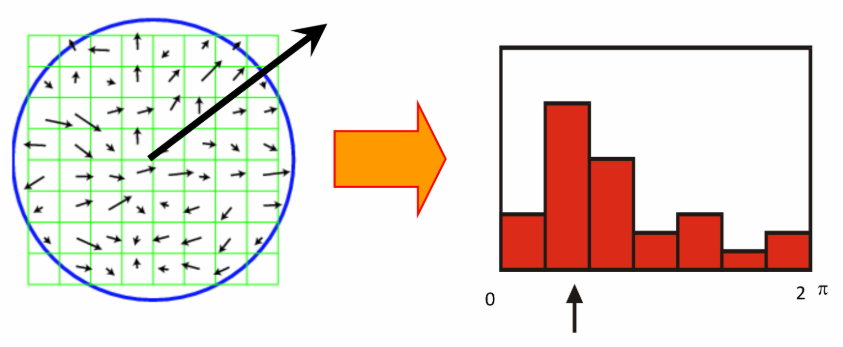
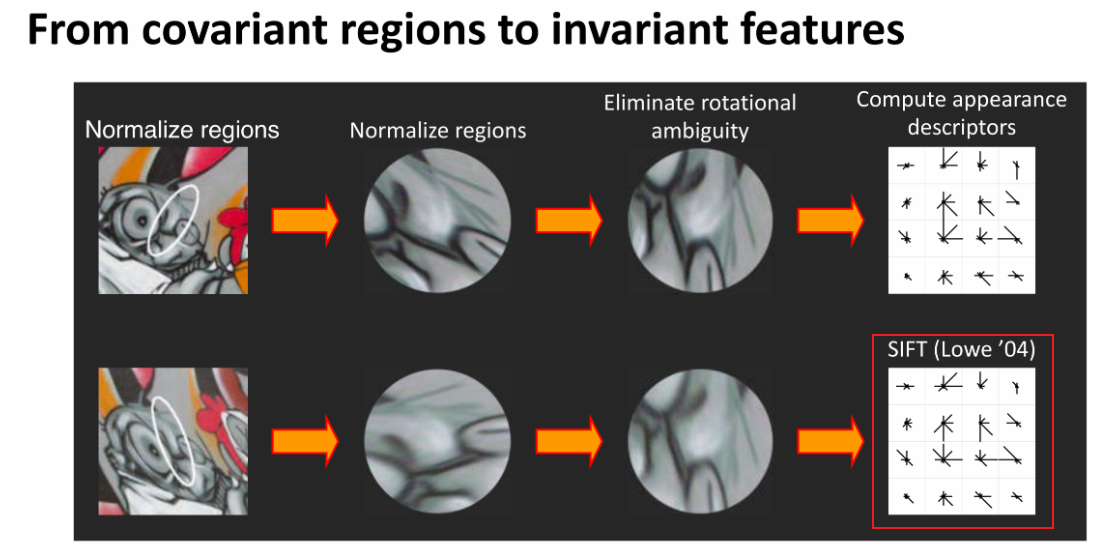
④ SIFT描述子

将小区域进行划分
1个区域划分为16个小区域，每个小区域存在8个方向，因此共有$16×8=128$维特征

3. 纹理特征

（1）纹理（Texture）

① 定义

某种基元以某种方式组合起来

② 分类

• 规则的纹理
• 不规则的纹理

③ 用途

• 从纹理中恢复形状信息
• 应用于分割、分类任务【课程主要关注】
  （可以帮助我们区分事物、划分类别等）
• 应用于合成任务

④ 纹理的重要性

• 通常表示了材料的特性
• 可能是重要的外观线索，特别是在物体形状相似的情况下
• 旨在区分形状、边界和纹理

（2）纹理特征的提取

① 发现模式（Pattern）

模式就是某种规则、规律

利用斑点检测器、角点检测器、边缘检测器…检测出基础的元素

② 描述纹理

利用统计的方法：平均值、标准差、直方图…

③ 示例

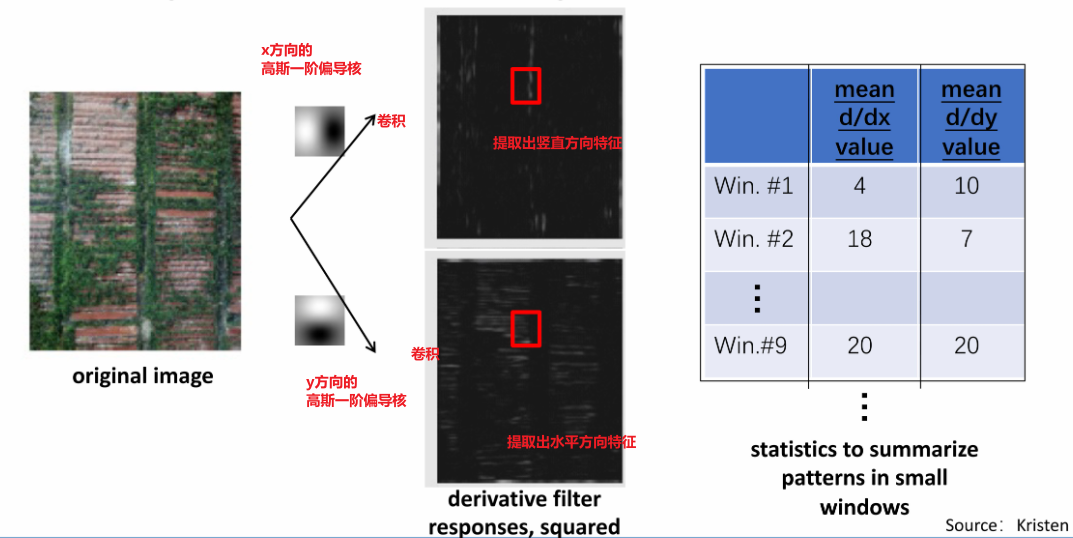
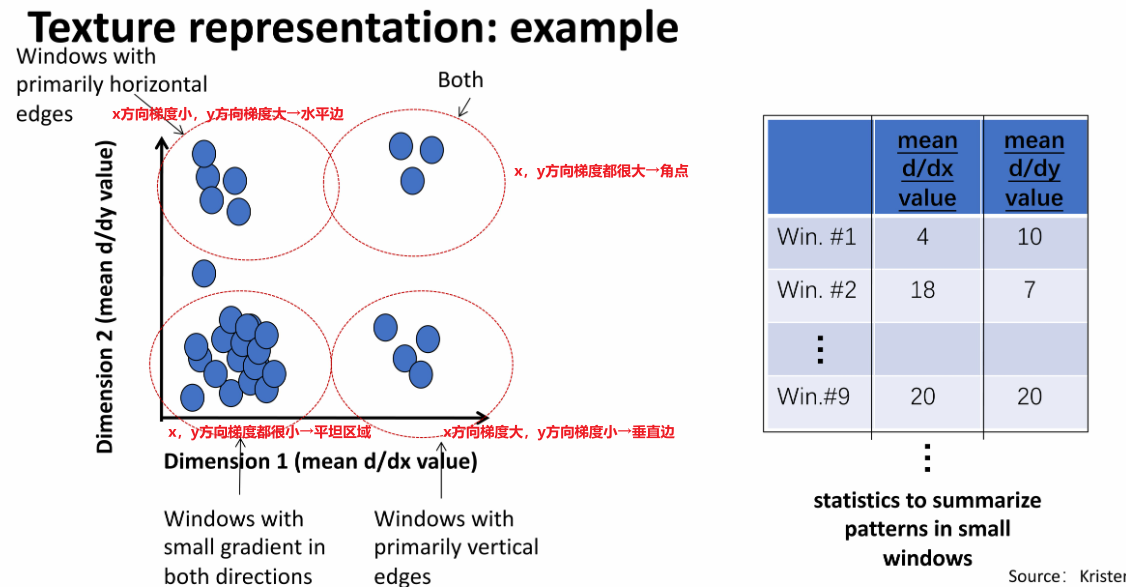
其中，

$D(a,b)=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2} = \sqrt{\sum_{i=1}^{3} (a_i - b_i)^2}$

④ Filter banks（滤波器组/卷积核组）

a. 背景

在③示例中，使用了两个滤波器分别在x和y两个方向上做卷积，产生了二维特征向量，用于描述窗口中的纹理特征。

b. 引入

推广，应用一组d个滤波器，产生d维特征向量

c. 形式

如图所示48维的滤波器组

每个窗口纹理被映射为48维空间的一个点，是一个48维的特征向量，这个点具有48维的特征

d. 多维高斯（Multivariate Gaussian）

展现了协方差矩阵和高斯核之间的关系：

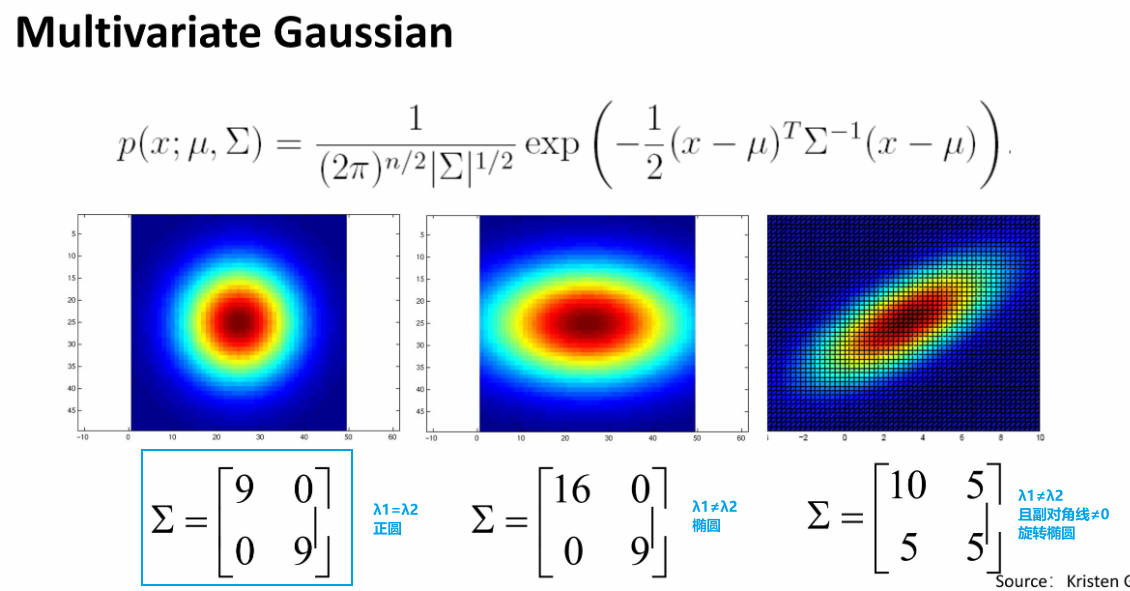
在 Filter banks中的48个滤波器就是通过如上编程定义（不同方向）

e. Filter bank 应用示例

应用一个38维的Filter bank做卷积：

一个匹配quiz：

f. Fliter bank 卷积结果的应用

i. 对整个图像卷积

一张图像，x维Filter bank卷积，得到x个卷积响应，对这x个卷积响应计算平均，得到了一个图像的x维特征向量，表示了图像

ii. 对每个像素点卷积

对一张图像的所有像素点，x维Filter bank卷积，每个像素得到x个卷积响应

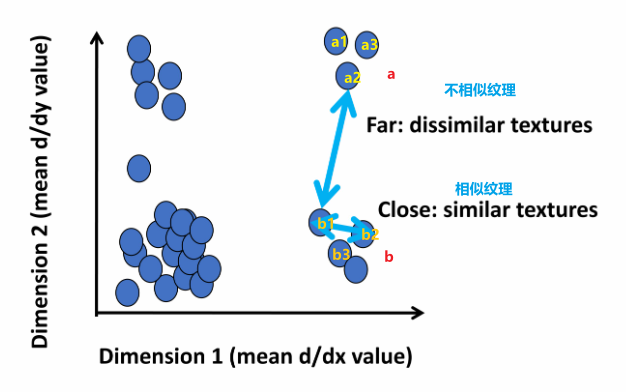
（3）纹理检测在视觉任务中的应用

• 通过Filter bank检索相似纹理 / 通过相似纹理的检索进一步进行图像分类任务
• 通过纹理来区分场景（其实也是分类任务）
• 通过纹理来进行图像分割，通过纹理让图像中的各部分进行了分类，从而分开了

七、分割

1. 图像分割的基本概念

（1）定义

将图像划分为多个互不相交的区域

（2）目标

根据像素的相似性，把具有相似特征的像素组织在一起，识别和分理处不同的对象或区域

（3）超像素

一个超像素=多个像素形成的小块，例如下图

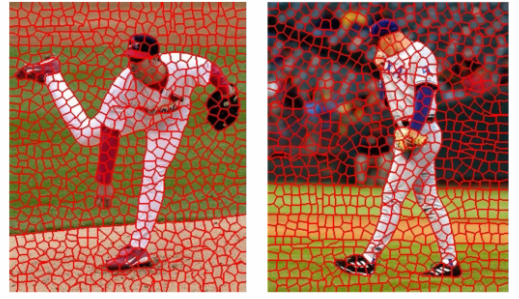
（4）理想的分割方法

既不是过分割，也不是欠分割

• 过分割：把一个主体过度分割成多个主体了
  （超像素属于一种过分割）
• 欠分割：没有完全分开，把多个主体划分成一个主体了

（5）分割方式

① 自下而上、自上而下

a. 自下而上的分割方法

• 自下：先获取像素的底层特征，例如纹理、边、点
• 而上：再分割出主体

b. 自上而下的分割方法

• 自上：先获取一定的图像语义等高层特征
• 而下：再分割出主体
  人思考的方式其实就是自上而下

② 有监督、无监督

• 有监督：给标签，从label中学习
• 无监督，没标签，自己寻找规律
  人思考的方式其实是有监督+无监督结合的
  常用深度学习模型基于有监督

2. 人类做图像分割的原理

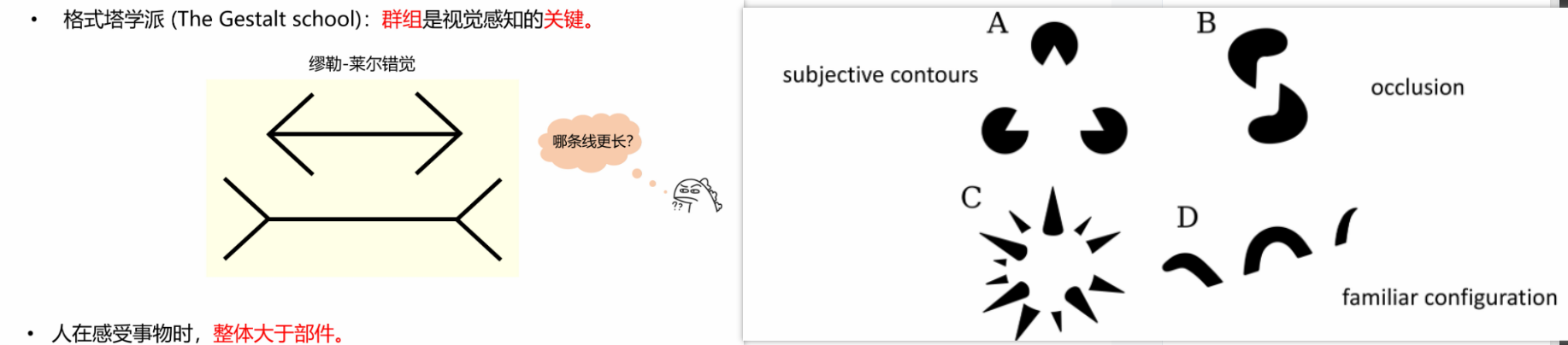
格式塔学派理论

群组是视觉感知的关键

（1）感知整体空间

人的视觉系统将元素综合为一个新的领域，相较于部件/元素，更感知整体

（2）利用先验知识做判断（自上而下）

例如下图，人类可能会根据经验，感觉到图像中的事物，比如中间有相交的道路

（3）格式塔的组织原则

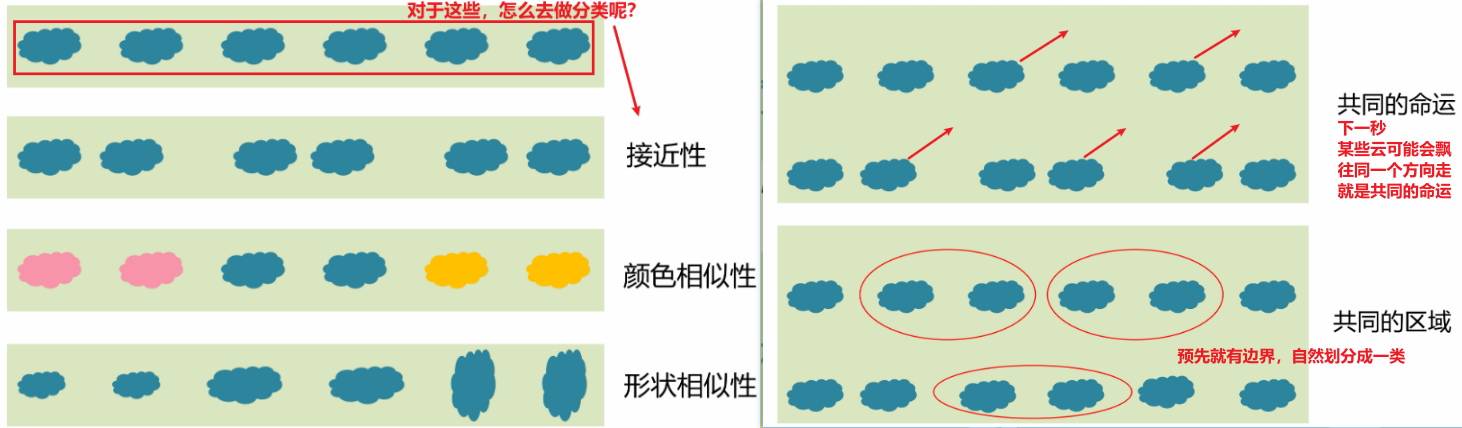
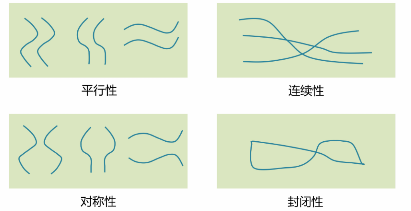
3. K-Means 图像分割

格式塔学派理论“群组”的思想，恰好对应机器学习的“聚类”任务

（1）算法流程

（2）应用实例及问题

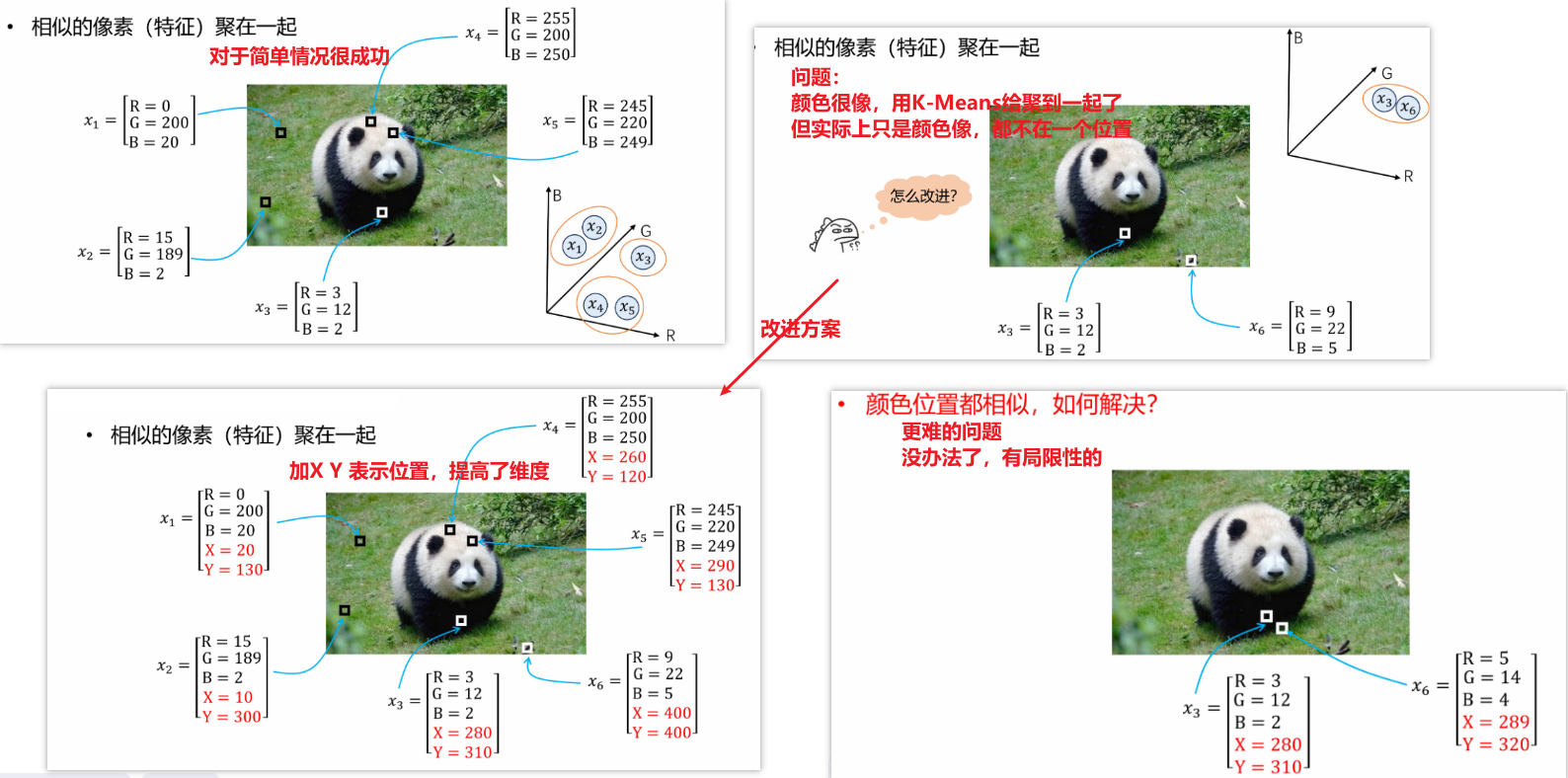
（3）影响因素

初始化聚类中心点的位置（位置不同，算法计算量不同，可能结果也不同）
聚类数量K的选取（图中K越大，效果越好，但在具体任务上也有可能出现别的问题，例如过分割~）

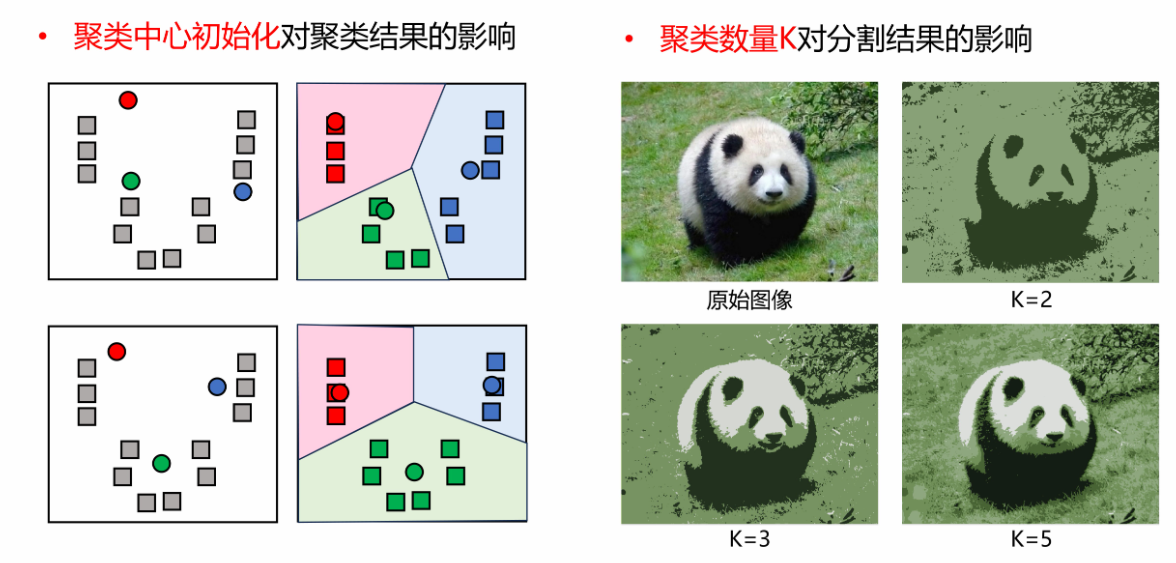
（4）优缺点

优点

• 非常简单
• 可以收敛到局部最优值
  缺点
• 内存需求较大
• 需要指定K的值，K值的选取影响结果
• 对初始化随机中心点位置十分敏感
• 对外点敏感
  
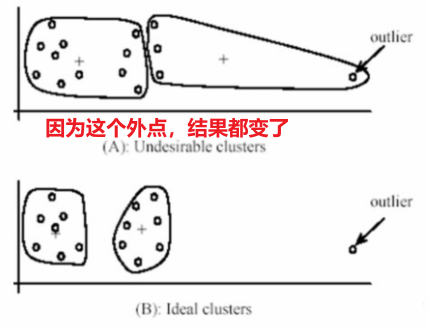
• 最终只能生成球形的聚类簇（因此在用K-Means时，需要看最终的任务形成的簇大概会是什么形状，K-Means 比较适合最终划分为球形簇的任务）

4. Mean Shift （均值漂移） 图像分割

（1）算法流程

原理：在特征空间中寻找密度模式，或密度的局部最大值
一步一步找到密度极大值点：

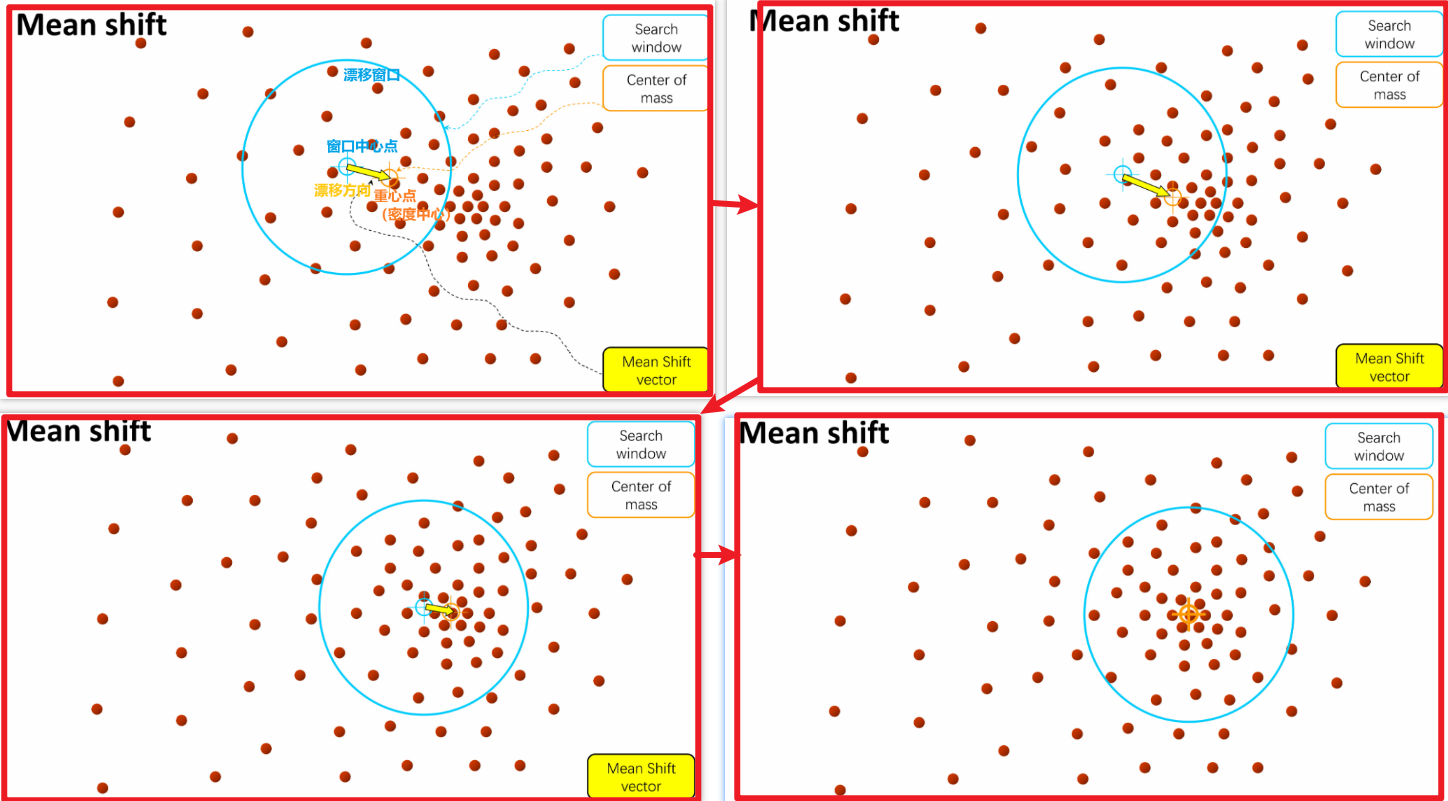
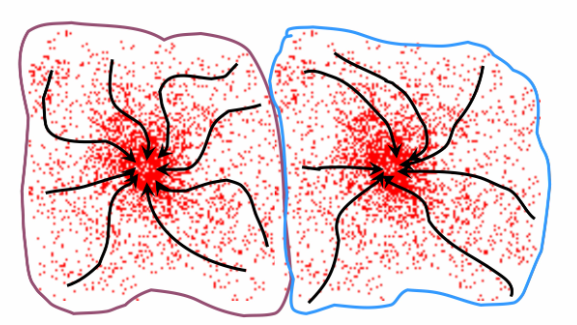
• 查找特征（颜色、纹理等）
• 在单个特征点初初始化漂移的窗口
• 对每个窗口执行均值漂移，直到收敛
• 合并最终接近相同峰值或模式的窗口
  

（2）优缺点

a. 优点

• 不需要假设聚类簇的一个球形的（不像K-Means那样），对任何形状都可以聚类
• 只需要设定一个参数——飘逸的窗口大小
• 不需要预先设定类别数量（K-Means里的K值），飘逸后找到几个点就代表几个类
• 对外点比较鲁棒

b. 缺点

• 最终输出的结果特别依赖于飘逸窗口大小的设置
• 计算成本高
• 如果特征维度太高，表现不太好了

c. 计算成本高的解决方案

• 对超像素进行Mean Shift，因为超像素本身已经是比较相似的像素的集合，对超像素进行均值漂移就不需要遍历图像中每一个像素了
• 记录每个漂移框漂移过程中涉及到的所有重心点，当其他框也飘到这个过程中的重心点时，则说明也是那个类（终点是一致的）

5. Graph Cut（图割）图像分割

（1）广义框架

移除一组边使图分裂为互不连通的子图

① 准备阶段

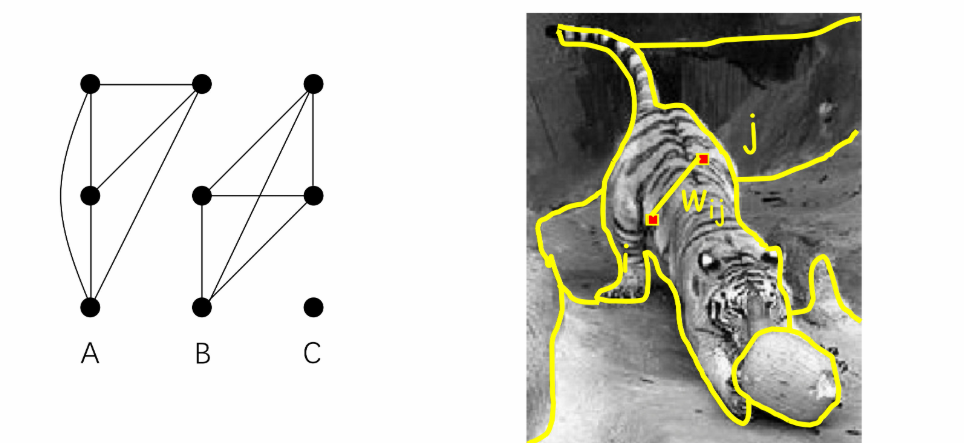
把图像表示成图结构：

• 节点：每个像素对应一个节点
• 边：相邻像素/满足空间邻近条件的像素对，通过边连接
• 边权重：像素对的相似性越高，权重越大
  
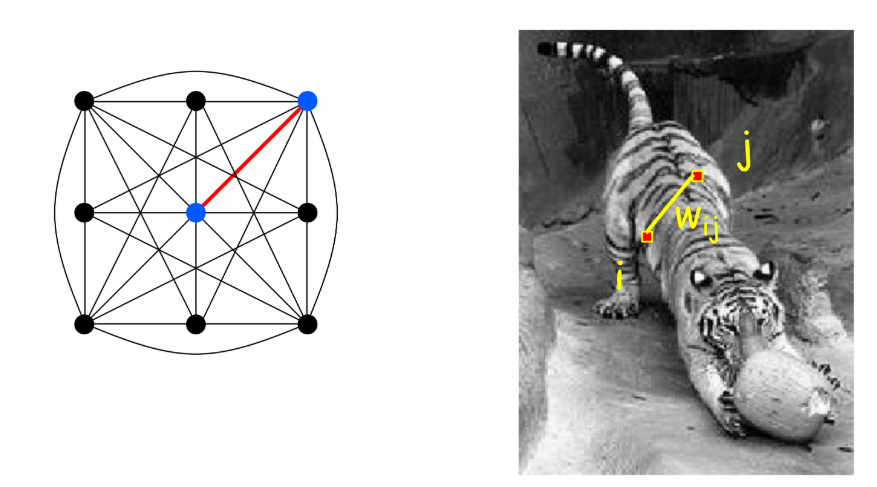
  权重涉及到的相似度计算：

$$\exp \left( -\frac{1}{2\sigma^2} \text{dist}(x_i, x_j)^2 \right)$$

像素表示为特征向量$x_i$，通过上面的公式，将特征向量间的距离映射为相似度（0到1之间）
其中：

• 距离可以用各种距离，例如欧氏距离，L2距离等
• $σ$ 控制相似性衰减速率，是一个尺度参数。
  • 小 $σ$：仅聚集邻近像素，生成细粒度分割（如纹理细节）
  • 大 $σ$：允许远距离像素归为同组，生成粗粒度分割（如整体轮廓）

② 割图阶段

断开图中的低权重边，将图划分为若干子图

（2）Minimum Cut（最小割）

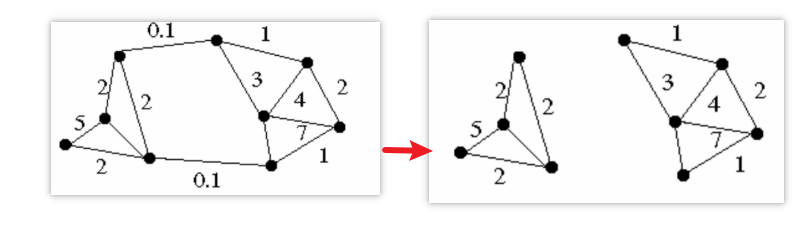
① 目标

割成本：被移除边的权重之和
因此最小割想要：找到使割成本最小的分割方式

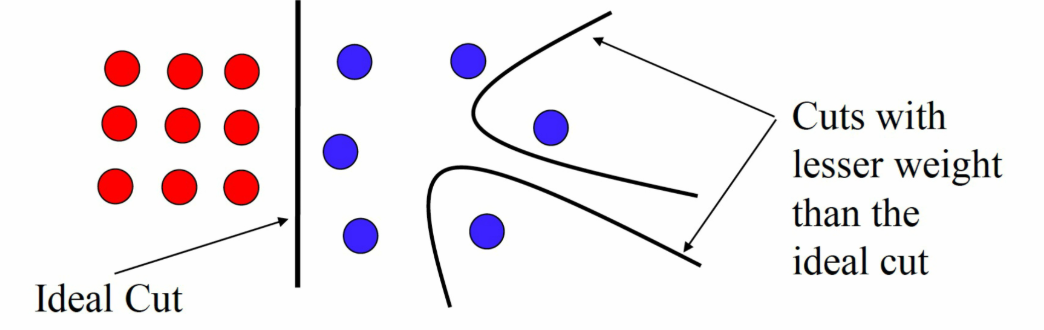
② 局限性

易切割出孤立小区域（如噪声点），导致过分割

（3） Normalized Cut（归一化割）

最小割倾向于割出很多小区域，这可以根据与每个区域相连所有边的总权重，通过引入归一化因子，平衡分割区域规模

① 原理

a. 归一化割的成本

归一化割成本公式：

$$\text{Normalized Cut Cost} = \frac{w(A, B)}{w(A, V)} + \frac{w(A, B)}{w(B, V)}$$

其中：

• $w(A,B)$：子图A与B间边权重和
• $w(A,V)$：子图A与全图V的边权重和
• $w(B,V)$：子图B与全图V的边权重和

矩阵表示：

$$\text{Normalized Cut Cost} ={\frac{y^T (D - W) y}{y^T D y}}$$

其中：

• $W$：图的邻接矩阵，$n×n$，元素 $W(i,j)$ 表示节点 $i$ 和 $j$ 之间边的权重
• $D$：一个对角矩阵，只有对角线上有值，且为 $D(i,i) = \sum_{j} {W}(i,j)$
• $D−W$：称为拉普拉斯矩阵，它反映了节点间的差异程度
• $y$：指示向量，用于标记每个节点所属的子集。如果第 $i$ 个节点属于子集 $A$，则 $y_i=1$，否则 $y_i$ 为一个负常数，通常设为 $-1$
• $y^T(D−W)y$：表示割的代价，即两个子集 $A$ 和 $B$ 之间的边权总和
• $y^TDy$：表示区域 $A$ 的总关联度，用于归一化分子部分，避免分割出孤立点或极小区域‘

b. 归一化割的数学松弛解法

i. 原理

直接求解归一化割成本的最优解（最小值）在计算上不可行（指数复杂度）
但可以通过放宽离散约束（允许指示向量 $y$ 取任意值），将问题转化为可解的广义特征值问题：

$$(D-W)y=\lambda Dy$$

解这个问题可以解出许多解：$(\lambda,y)$
我们的最终目标：拿到第二小特征值($\lambda$) 所对应的解的 $y$ 值
（第一小特征值是 $λ=0$，对应特征向量 $y=[1,1,...,1]^T$，所有像素归为同一类，无意义）
这个 $y$ 的值表示了像素的分组倾向，可以根据 $y$ 值分布，使用0或中位数来进行分类（割一刀）（属于哪个子集）

可以这样理解：平常 $y_i$可能只能取 $+1$ 或 $-1$，但我们可以放宽要求，让 $y_i$ 取任意的正负值，这样就不是绝对二分类，而是类似于对于某个子集的置信度得分（更加可能属于哪个子图）

ii. 算法流程

• 构建图：将图像表示为带权的图 $G=(V,E)$ （节点可能是像素或者超像素），并计算每条边的权重，得到边权重矩阵 $W$ 和 对角矩阵 $D$
• 特征求解：计算 $(D-W)y=\lambda Dy$ 的第二小特征向量 $y$
• 割：根据特征向量 $y$ 元素值的分布进行阈值分割

iii. 扩展到多类割

现在的割是一图割两半
也可以扩展到一图一次多割
方法有：

• 递归二分：逐层细分（可能引入误差累积）
• K-Means聚类：联合多个特征向量（前k个）进行聚类

c. 效果

效果不错捏

d. 利用纹理特征进行分割

如何分割那些是“纹理马赛克”的图像（反正就是因为纹理的问题搞得有点难分割的图像）

步骤：

• 用一组滤波器组（Filter Bank）对图像进行卷积，提取不同方向和尺度下的纹理特征响应
• 对所有得到的纹理特征响应，使用聚类算法对特征进行分组，每个聚类中心对应一种纹理的基元
• 统计窗口内所有像素的纹理基元类别分布，生成基元直方图，直方图的每个bin对应一种基元出现的频率
• 基元直方图将用于归一化割之中，例如可通过基元直方图来构建 $W$ 矩阵等

不过还可能有一种特殊情况：相似纹理跨不同物体（如鹰的羽毛与背景纹理混淆）
解决策略：介入轮廓检测。在计算像素间亲和度时，沿连接路径检查是否存在显著边缘（如Canny边缘）

e. 归一化割的优缺点

优点：是一个通用的框架，算法流程清晰、固定，可以结合很多其他特征和相似度计算工作
缺点：图像存储要求高（不过可以用超像素缓解）、时间复杂度高、倾向于把一个图分为两个部分（如果想得到多个可能需要再多次执行归一化割算法）

6. 基于深度学习的弱监督图像分割

有如下几种标住手段，从而不用一点一点描边缘：

八、识别

1. 图像识别基本概念

（1）涉及到的任务

• 分类：二分类、多分类
• 检测：包含两个部分：定位+分类（先得到位置信息，再判断是啥东西）
• 分割；语义分割（例如，结合了语义描述，某个类别是人，另一个类别是狗。。）、实例分割（人和人不一样，小美小帅）
• 类别识别和单实例识别
• 行为或事件识别

理解单实例：就比如拍了个华电西门，虽然都是门，但是花店西门跟别人家学校的门不一样，它就是门的一个单独的实例，具体它自己独立的含义~

（2）图像识别算法应当解决的问题

• 对图像或视频进行分类（视频可以切成帧来做分类任务）
• 对物体进行检测和定位
• 评估语义和几何特征
• 分析人类的行为和事件

（3）图像识别的难点

• 种类问题——世界上那么多种类的事物，怎么才能学习到这么多种
• 视角问题——从不同的视角得到的同一个图像，怎么才能识别成功
• 光照问题——同一个图像的光照不同，怎么才能识别成功
• 尺度问题——怎么让算法能够对抗尺度变化（缩放）
• 形变问题——怎么让算法能够对抗形状的变化（一只小猫咪、一坨小猫咪、一条小猫咪、一摊小猫咪…）
• 遮挡问题——怎么让算法能够对抗遮挡（带了口罩怎么才能认出我是我）
• 背景杂波问题——长得跟背景也太像了，咋区分呢，像下图这样
  
• 人为设计问题——同样是椅子，有好多种设计形态呢，设计师灵感不灭，椅子形态总会更新

2. 图像识别算法设计

（0）设计识别算法需要考虑的问题

• 表达：怎么表达图像类别
• 学习：怎么学习给定的数据，得到模型
• 识别：怎么在崭新的数据上应用学习好的模型

（1）表达–Representation

① 表达的方式

先划分成小块，有下面很多种划分成小块的方式：

然后放入一个词袋中（像一块拼图），可附加一些语义信息等（每个小块之间可能有关联，从而能根据这些关联拼凑出要识别的东西），拼凑出识别物体，从而表达了图像

② 理想的表达能具备的效果

不变性（Invariance）

视角不变性、光照强度不变性、遮挡不变性、尺度不变性、形变不变性、背景杂波不变性…

③ 图像识别任务选取的模型

对于这种内类的变化（同一类别中不同样本之间的差异性，比如对于猫类，有狸花猫、布偶猫、奶牛猫…），概率模型更为有效
概率模型有下面三种

a. 生成式模型（Generative Model）

区分张三和李四，先知道他们都具体长啥样，然后区分开

思想：建模数据本身的分布，学习“如何生成这个类别的样本”
根据先验（自然本身就有的规律）和似然来建模
常见模型：朴素贝叶斯、层次化贝叶斯（潜在迪利克雷分布）…

b. 判别式模型（Discriminative Model）

区分张三和李四，不管他俩长啥样，只要找到一个差异能分开他俩就行

思想：直接学习类别之间的边界，不关心数据如何生成
根据后验（从结果观察到总结出的规律）来建模
常见模型：近邻分类法、神经网络、支持向量机及其衍生算法、Boosting…

④ BoF（Bag of Features）方法

借鉴了文本处理中的词袋BoW（Bag of Words）模型，将图像视为由多个局部特征组成的集合，类似于文档中的词汇

a. 步骤

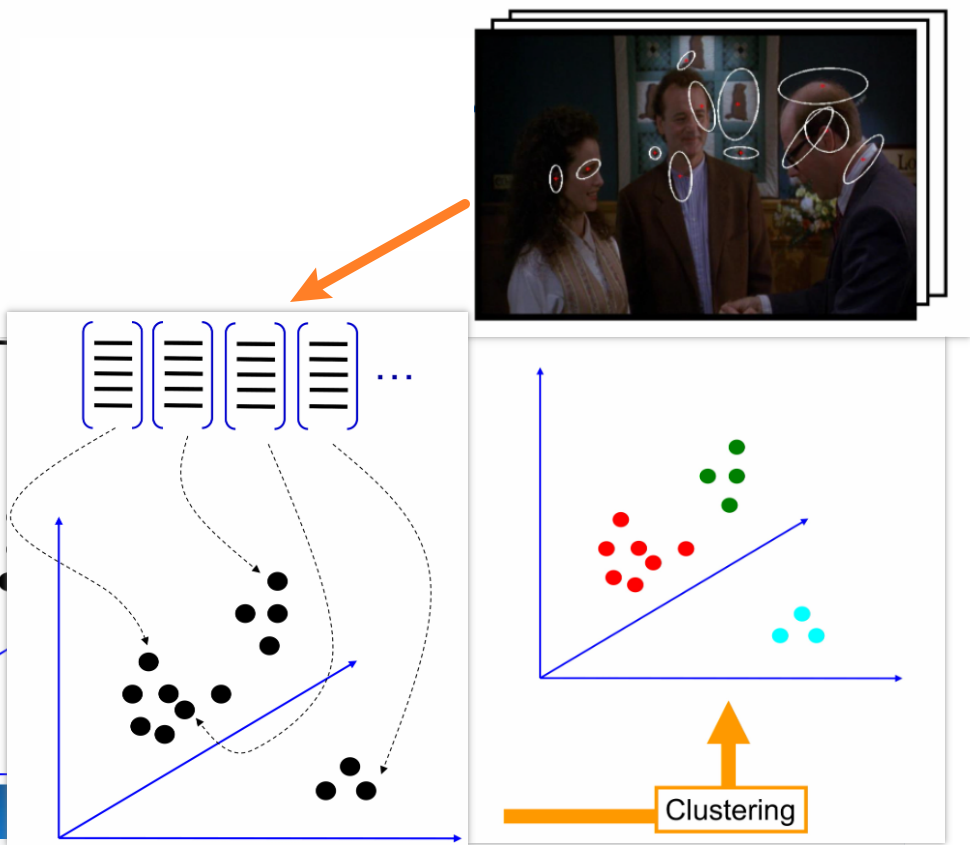
i.特征提取

• 先提取图像特征，可以用规则网格，也可以用显著性检测只提取感兴趣区域
  
• 根据提取到的特征，用聚类算法（例如K-Means）进行聚类
  

ii. 学习“视觉词汇”

码本生成（Codebook Learning）：刚才聚类得到的每个特征向量聚簇的聚类中心，称为码向量（Codevector），即视觉词汇；所有码向量构成码本（Codebook），即视觉词汇表（Visual Vocabulary）

涉及的问题与解决：

• 词汇量选择：
  • 过小：视觉词无法覆盖所有特征（如蝴蝶翅膀纹理差异被忽略）
  • 过大：量化噪声增加（相似特征被分到不同类），导致过拟合
• 传统K-means聚类随词汇量增长计算量激增

解决：

• 词汇树（Vocabulary Trees, Nister & Stewenius, 2006）：分层聚类结构，通过树状搜索加速最近邻匹配

iii. 用“视觉词”频率表示图像

• 码本（视觉词汇表）可以表示图像
• 将新特征映射到码本中最接近的码向量索引（离散化表示），例如：特征向量→索引3（代表“车轮”视觉词）

c. 混合模型（Hybrid Model）

思想：结合生成式与判别式模型的优势
平衡先验与后验，通过隐变量或联合优化融合两类模型优势

（2）学习-- Learning

关注的问题有：

• 学习参数
• 监督信息的级别（手动分割、边界框、图像打标签、噪声标签）
• 批量（batch）/增量（incremental）
• 先验（领域知识、专业知识）
• 训练时可能遇到的问题：过拟合、负样本

批量学习：一次性加载全部训练数据（如10000张图片），完成整个数据集遍历后才更新模型参数
增量学习：逐步接收新数据（如每天新增100张图片），每接收一个/小批样本就立即更新
负样本是指与目标类别相反的参照数据。它们的作用是帮助模型建立区分边界，通过对比学习使模型更精准地识别正样本。

（3）识别-- Recognition

① 识别任务

见1.（1）

② 搜索策略

滑动窗口，通过不同尺度（S）、位置（x,y）、旋转角度（θ）的窗口遍历图像

③ 搜索策略存在的问题

a. 计算复杂度

窗口数=位置(x,y)×尺度(S)×角度(θ)×类别(N)，导致计算量爆炸
解决：

• Lampert et al. BSW (2008)：基于分支定界法（Branch and Bound）的 BSW (Branch-and-Bound with Subwindows) 方法，通过智能剪枝减少无效窗口计算
• Alexe et al. (2010)：改进候选区域生成（Objectness），预筛无关区域提升效率

b. 定位困难

传统检测方法默认用矩形框（Bounding Box）标注物体，但实际物体形状复杂（如弯曲的动物肢体、树枝、服装褶皱等）
矩形框无法贴合非规则物体边缘，且滑动窗口可能将相似纹理/颜色的背景区域误判为物体，导致误报
解决：

• 非极大值抑制 NMS：合并重叠检测框，仅保留置信度最高的结果
• 用Canny边缘检测辅助：通过提取物体边缘轮廓（如狗与背景的边界），辅助判断检测框是否贴合真实形状（减少“框住空气”的误报）
• 引入语义分割技术：不再依赖矩形框，而是逐像素标注物体所属类别（如“狗”像素 vs “人”像素）

九、检测

聚焦于图像的位置→找一个模板，在图像中滑动窗口检测，区分是否存在我们要找的对象
【检测任务→分类任务（每个框是否有我们要找的对象）】

1. 目标检测的难点

（1）可能遇到的问题

可能受以下影响：

• 光照强度
• 物体的姿势
• 背景杂波
• 遮挡
• 视角
• 非物体（即其他部分如背景）干扰
• 目标特征相似度
• …

（2）设计算法需要解决的问题

① 如何高效搜索可能的对象

可能需要成千上万的窗口，计算量庞大，怎么办

② 特征的设计和评分

• 外观如何建模
• 哪些特征与要检测的对象有联系

③ 怎么处理不同的视角

• 传统为不同的视角建立各自的检测模型

2. 人脸检测 （Face Detection）

（1）

基于滑动窗口法的人脸检测：

• 一方面，框不断滑动位置，寻找人脸
• 另一方面，框也会不断更改尺寸，因为不知道人脸在图像中的大小
  

（2）人脸检测的难点

① 滑动窗口计算量庞大

成千上万的位置，太多了
解决：由于人脸在图像中是少量的，为了提高计算效率，希望在非面部窗口上花的时间越少越好

② 怎么降低假阳性（False Positive）

False Positive：把不是人脸的检测成人脸了

（3）Viola & Jones算法

基于boosting原理的人脸检测

① Boosting

a. 为什么选用Boosting

• 能得到较鲁棒的分类器，且简单
• 是一个提供稀疏视觉特征选择的有效算法
• 易于实现，不需要外部优化工具、

b. 原理

图示：

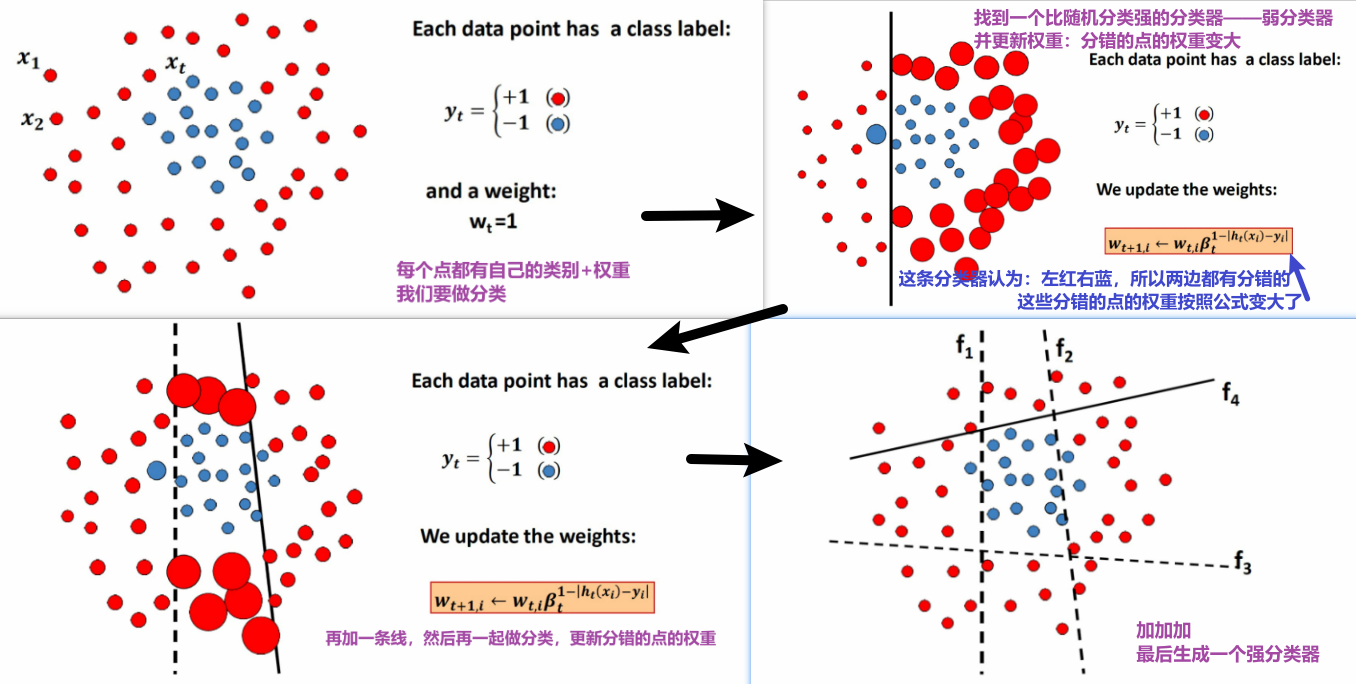
公式：

其中：

② Viola & Jones算法核心特性

• 实时目标检测的"范式级"方法
• 训练过程缓慢（需处理大量数据），但检测速度极快（适合实时应用）

③ Viola & Jones算法流程

a. 用积分图加速特征提取并获取弱分类器

如图的四种矩形可以通过计算黑白区域像素差，来捕捉图像特征

特征太多了，24x24窗口内16万种特征，每个特征需遍历矩形内所有像素求和，直接计算每个特征的时间复杂度为O(n)，太耗时，于是我们采用下面的积分图加速：
积分图每个点(x,y)存储的是其左上角所有像素值的和
$I_{\sum}(x, y) = \sum_{x' \leq x, y' \leq y} i(x', y')$

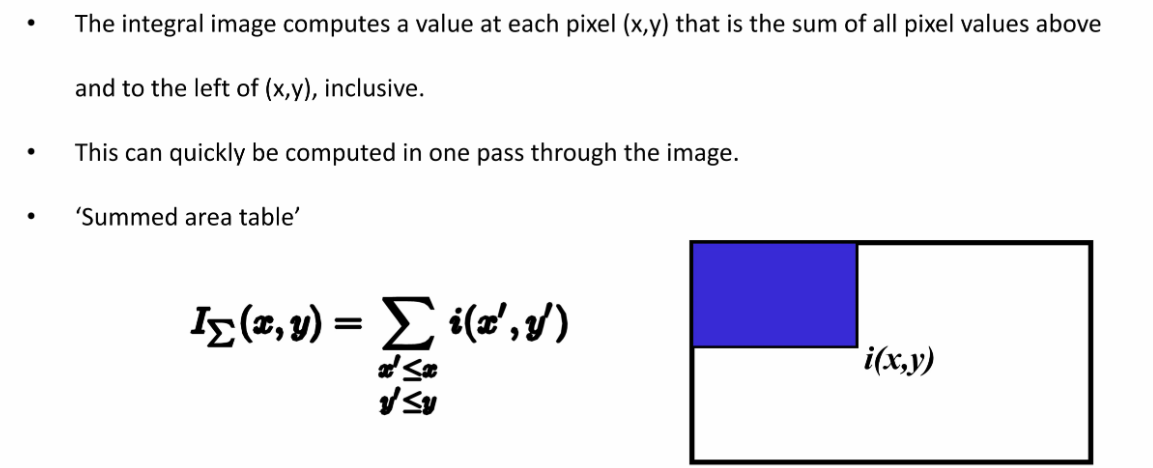
则对于任意矩形区域，就可以很快求得积分值了：

b. 引入Boosting思想构建强分类器

i. 构建最优弱分类器–最优滤波器+阈值组合

针对每个矩形特征（如$α₁$），计算其在所有样本上的响应值（$fⱼ(x)$）是否大于阈值 $\theta _j$，是则 $h_j(x)=1$，否则$h_j(x)=0$

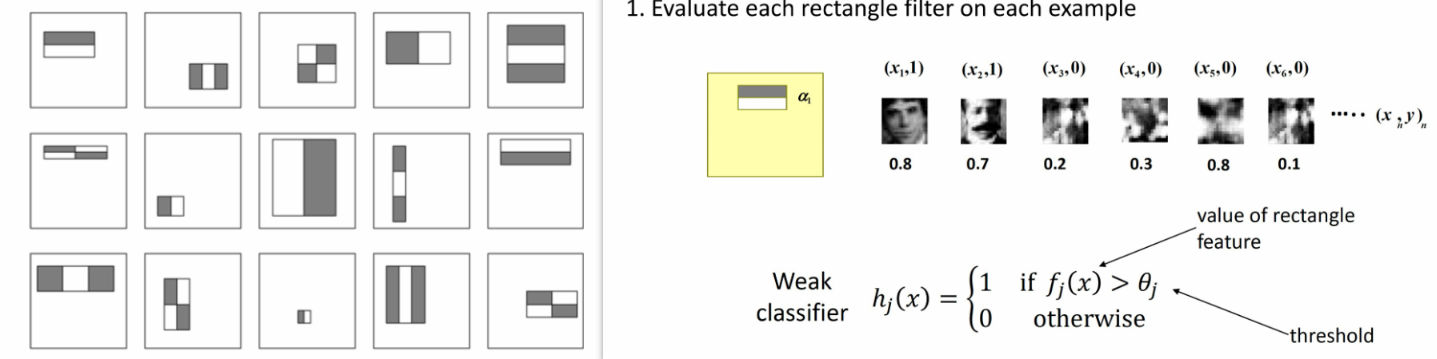
对权重归一化：$w_{t,i} \leftarrow \frac{w_{t,i}}{\sum_{j}^{n} w_{t,j}}$
对每个滤波器 $j$，计算所有样本的特征值 $fⱼ(x)$，并遍历候选 $θ$，选择使分类误差最小的 $θⱼ$
对每个$hⱼ(x)$和对应的$θⱼ$，计算其在当前权重下的误差$εⱼ$

$$\varepsilon_j = \sum_{i} w_i |h_j(x_i) - y_i|$$

选择 $εⱼ$ 最小的 $hⱼ(x)$ 作为本轮最优弱分类器 $hₜ$

ii. 重新设置权重

计算调整因子 $βₜ$ ：

$$\beta_t = \frac{\varepsilon_t}{1 - \varepsilon_t}$$

更新样本权重：

$$w_{t+1,i} \leftarrow w_{t,i} \beta_t^{1 - |h_t(x_i) - y_i|}$$

解读一下 $βₜ$ 的意义：
对第 $t$ 个样本的，当前弱分类器表现很差（误差大），那么我们是想要让这些分类错误的样本在后面更受关注，分类正确的就不管了，所以如果 $\epsilon _t$ 很小（分的对），那么就应该让它的权重变小。
我们的公式，如果 $\epsilon _t$ 很小，$βₜ → 0$，再看更新样本权重的公式，就可以看出正确样本的权重很小了，则错误样本的权重就相对来说大了。
注意，这里并不是提高了错误样本的权重，而是降低正确分类样本的权重。

iii. 得到强分类器

$$h(x) = \begin{cases} 1 & \sum_{t=1}^{T} \alpha_t h_t(x) > \frac{1}{2} \sum_{t=1}^{T} \alpha_t \\ 0 & \text{otherwise} \end{cases}$$

其中：$\alpha_t = \log \frac{1}{\beta_t}$，$\beta_t = \frac{\varepsilon_t}{1 - \varepsilon_t}$

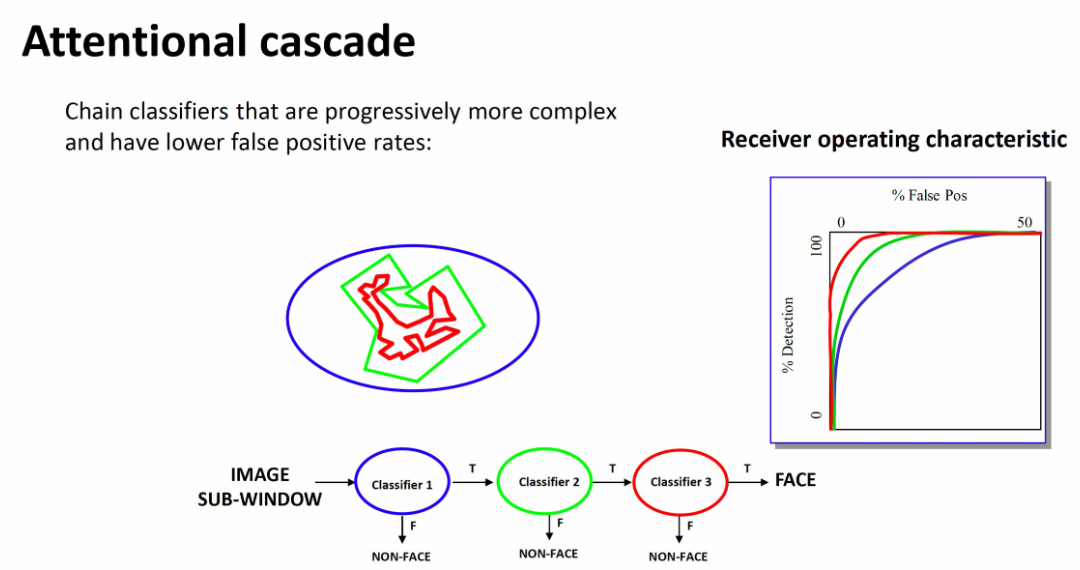
c. 利用注意力级联机制快速去除负样本

是一个逐步筛除的过程：

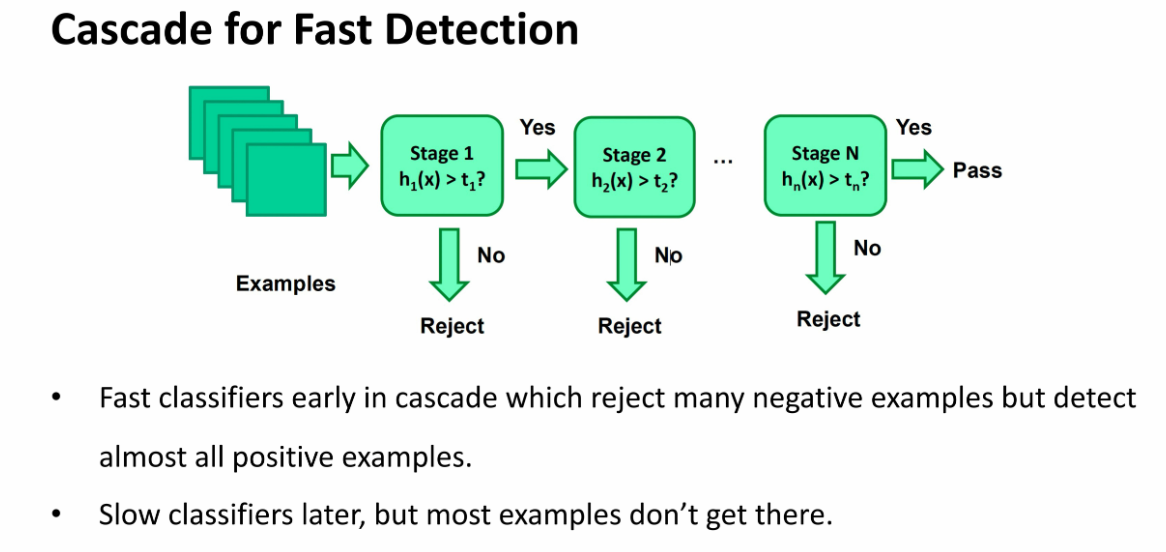
简单来说，就是一次比一次精细，每次只关注上次不确定的那些样本，这样能够在最开始快速去除很多负样本,并一点一点逐渐降低误报：

3. 行人检测（Pedestrian Detection）

（1）HOG特征

HOG特征（方向梯度直方图，Histogram of Oriented Gradients） 是一种用于目标检测的传统图像特征描述方法，由Navneet Dalal和Bill Triggs于2005年提出，尤其在行人检测领域表现突出。其核心思想是通过统计图像局部区域的梯度方向分布来描述物体轮廓和形状特征。

（2）Dalal-Triggs 行人检测流程

① 滑动窗口提取

在多尺度图像金字塔上，以64x128窗口滑动遍历所有位置

② HOG特征计算

计算方式PPT里没有，但在这里写一下：

1.图像预处理：

• 转为灰度图，并进行伽马校正（减少光照影响）。
• （可选）调整图像尺寸，统一输入尺度。

2.计算梯度：

• 使用水平 ($G_x$) 和垂直 ($G_y$) 方向的Sobel算子计算每个像素的梯度：
  梯度幅值 = $\sqrt{G_x^2 + G_y^2}$, 梯度方向 = $\arctan\left(\frac{G_y}{G_x}\right)$

3.划分细胞单元（Cell）：

• 将图像划分为多个小单元（如8×8像素的Cell）。
• 对每个Cell内的像素，统计其梯度方向直方图（通常分为9个方向区间，即0°~180°或0°~360°）。

4.块（Block）归一化：

• 将相邻的多个Cell组合成一个Block（如2×2的Cell组成16×16像素的Block）。
• 对Block内所有Cell的直方图进行归一化（如L2归一化），增强对光照和对比度的鲁棒性。

5.生成特征向量：

• 所有Block的归一化直方图按顺序拼接，形成最终的高维特征向量（例如，64×128的图像按8×8 Cell划>分，每个Block滑动步长8像素，最终特征维度为7×15×36=3780）

对每个窗口提取3780维HOG特征

③ 线性SVM分类

使用预训练的SVM权重向量w对窗口打分（：$Score=w^T⋅HOG特征向量+b$）
分数高于阈值则判定为行人

④ 非极大值抑制

在连续响应图上寻找局部最大值，合并重叠检测框

4. 统计模板方法的优缺点

统计模板方法是一类基于手工设计特征与统计学习的目标检测/识别算法，通过分析目标在图像中的统计分布规律（如边缘方向、纹理对比度），构建数学化的特征模板，并利用分类器（如SVM、Adaboost）进行匹配决策。其核心特点是数据驱动但依赖人工先验知识
例如上面的HOG+SVM、Viola-Jones

（1）优点

• 在检测具有标准方向（典型、固定的视角等）的非可变形对象（人脸、汽车、行人）的任务上，表现不错
• 检测很快

（2）缺点

• 对于高度可变形的事物（比如猫咪，太软了啥形态都有），检测效果可能不太好
• 抗遮挡能力不强
• 需要大量的训练数据

十、跟踪

考试不考，时间精力原因暂不梳理